题目内容
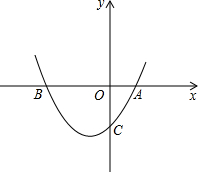
如图,一次函数y=-4x-4的图象与x轴、y轴分别交于A、C两点,抛物线y=
x2+bx+c的图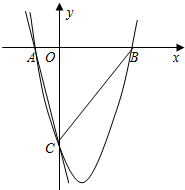 象经过A、C两点,且与x轴交于点B.
象经过A、C两点,且与x轴交于点B.
(1)求抛物线的函数表达式;
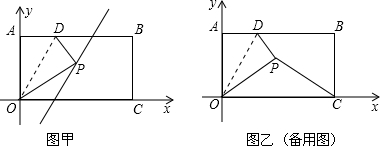
(2)设抛物线的顶点为D,求四边形ABDC的面积;
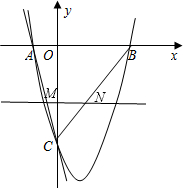
(3)作直线MN平行于x轴,分别交线段AC、BC于点M、N.问在x轴上是否存在点P,使得△PMN是等腰直角三角形?如果存在,求出所有满足条件的P点的坐标;如果不存在,请说明理由.
| 4 |
| 3 |
 象经过A、C两点,且与x轴交于点B.
象经过A、C两点,且与x轴交于点B.(1)求抛物线的函数表达式;
(2)设抛物线的顶点为D,求四边形ABDC的面积;
(3)作直线MN平行于x轴,分别交线段AC、BC于点M、N.问在x轴上是否存在点P,使得△PMN是等腰直角三角形?如果存在,求出所有满足条件的P点的坐标;如果不存在,请说明理由.
(1)∵一次函数y=-4x-4的图象与x轴、y轴分别交于A、C两点,
∴A(-1,0)C(0,-4),
把A(-1,0)C(0,-4)代入y=
x2+bx+c得
∴
,解得
,
∴y=
x2-
x-4;
(2)∵y=
x2-
x-4=
(x-1)2-
,
∴顶点为D(1,-
),
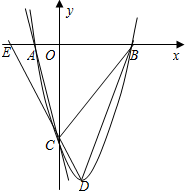
设直线DC交x轴于点E,
由D(1,-
)C(0,-4),
易求直线CD的解析式为y=-
x-4,
易求E(-3,0),B(3,0),
S△EDB=
×6×
=16,
S△ECA=
×2×4=4,
S四边形ABDC=S△EDB-S△ECA=12;
(3)设M、N的纵坐标为a,
由B和C点的坐标可知BC所在直线的解析式为:y=
x-4,
则M(
,a),N(
,a),
 ①当∠PMN=90°,MN=a+4,PM=-a,因为是等腰直角三角形,则-a=a+4则a=-2则P的横坐标为-
①当∠PMN=90°,MN=a+4,PM=-a,因为是等腰直角三角形,则-a=a+4则a=-2则P的横坐标为-
,
即P点坐标为(-
,0);
②当∠PNM=90°,PN=MN,同上,a=-2,则P的横坐标为
=
,
即P点坐标为(
,0);
③当∠MPN=90°,作MN的中点Q,连接PQ,则PQ=-a,
又PM=PN,∴PQ⊥MN,则MN=2PQ,即:a+4=-2a,
解得:a=-
,
点P的横坐标为:
=
=
,
即P点的坐标为(
,0).
∴A(-1,0)C(0,-4),
把A(-1,0)C(0,-4)代入y=
| 4 |
| 3 |
∴
|
|
∴y=
| 4 |
| 3 |
| 8 |
| 3 |
(2)∵y=
| 4 |
| 3 |
| 8 |
| 3 |
| 4 |
| 3 |
| 16 |
| 3 |
∴顶点为D(1,-
| 16 |
| 3 |
设直线DC交x轴于点E,
由D(1,-
| 16 |
| 3 |
易求直线CD的解析式为y=-
| 4 |
| 3 |
易求E(-3,0),B(3,0),
S△EDB=
| 1 |
| 2 |
| 16 |
| 3 |
S△ECA=
| 1 |
| 2 |
S四边形ABDC=S△EDB-S△ECA=12;
(3)设M、N的纵坐标为a,
由B和C点的坐标可知BC所在直线的解析式为:y=
| 4 |
| 3 |
则M(
| -4-a |
| 4 |
| 3a+12 |
| 4 |
 ①当∠PMN=90°,MN=a+4,PM=-a,因为是等腰直角三角形,则-a=a+4则a=-2则P的横坐标为-
①当∠PMN=90°,MN=a+4,PM=-a,因为是等腰直角三角形,则-a=a+4则a=-2则P的横坐标为-| 1 |
| 2 |
即P点坐标为(-
| 1 |
| 2 |
②当∠PNM=90°,PN=MN,同上,a=-2,则P的横坐标为
| 3×(-2)+12 |
| 4 |
| 3 |
| 2 |
即P点坐标为(
| 3 |
| 2 |
③当∠MPN=90°,作MN的中点Q,连接PQ,则PQ=-a,
又PM=PN,∴PQ⊥MN,则MN=2PQ,即:a+4=-2a,
解得:a=-
| 4 |
| 3 |
点P的横坐标为:
| ||
| 2 |
| a+4 |
| 4 |
| 2 |
| 3 |
即P点的坐标为(
| 2 |
| 3 |


练习册系列答案
相关题目

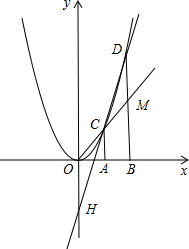 线OC交BD于点M,直线CD交y轴于点H,记点C、D的横坐标分别为xC、xD,点H的纵坐标为yH.
线OC交BD于点M,直线CD交y轴于点H,记点C、D的横坐标分别为xC、xD,点H的纵坐标为yH.