题目内容
已知y=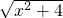 +
+ ,则y的最小值是________.
,则y的最小值是________.
5
分析:作线段AB=4,作线段AC⊥AB,且AC=1,作BD⊥AB,且BD=2,并且D和C在AB的两侧,过D作DM∥AB,交CA的延长线于M,连接CD交AB于E,则此时CE+DE最小,设BE=x,求出CE和DE的长,在△CMD中,CM=3,MD=4,求出CD,即CE+DE的最小值是CD,即可得出答案.
解答:作线段AB=4,
作线段AC⊥AB,且AC=1,作BD⊥AB,且BD=2,并且D和C在AB的两侧,过D作DM∥AB,交CA的延长线于M,
在直线AB上任取一点E,显然有CE+DE≥CD,
即当连接CD交AB于E,此时CE+DE=CD,
这时CD的长就是AC+BD的最小值.,
设BE=x,在Rt△DBE中,DE=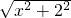 =
=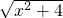 ,
,
同理DE= =
= ,
,
在Rt△CMD中,MC=MA+AC=BD+AC=1+2=3;DM=AB=4,
CD= =
= =5,
=5,
即y的最小值是CD=5,
故答案为:5.
点评:本题考查了轴对称-最短路线问题和勾股定理的应用,此题比较好,但是一道难度偏大的题目,对学生提出较高的要求.
分析:作线段AB=4,作线段AC⊥AB,且AC=1,作BD⊥AB,且BD=2,并且D和C在AB的两侧,过D作DM∥AB,交CA的延长线于M,连接CD交AB于E,则此时CE+DE最小,设BE=x,求出CE和DE的长,在△CMD中,CM=3,MD=4,求出CD,即CE+DE的最小值是CD,即可得出答案.
解答:作线段AB=4,

作线段AC⊥AB,且AC=1,作BD⊥AB,且BD=2,并且D和C在AB的两侧,过D作DM∥AB,交CA的延长线于M,
在直线AB上任取一点E,显然有CE+DE≥CD,
即当连接CD交AB于E,此时CE+DE=CD,
这时CD的长就是AC+BD的最小值.,
设BE=x,在Rt△DBE中,DE=
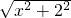 =
=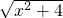 ,
,同理DE=
 =
= ,
,在Rt△CMD中,MC=MA+AC=BD+AC=1+2=3;DM=AB=4,
CD=
 =
= =5,
=5,即y的最小值是CD=5,
故答案为:5.
点评:本题考查了轴对称-最短路线问题和勾股定理的应用,此题比较好,但是一道难度偏大的题目,对学生提出较高的要求.

练习册系列答案
相关题目
已知 是整数,则x的最小整数值是( )
是整数,则x的最小整数值是( )
| A.16 | B.±16 | C.25 | D.±25 |
 是整数,则x的最小整数值是( )
是整数,则x的最小整数值是( ) 是整数,则n的最小整数值是________________
是整数,则n的最小整数值是________________ 是整数,则n的最小正整数值是 .
是整数,则n的最小正整数值是 . 是整数,则n的最小正整数值是 .
是整数,则n的最小正整数值是 .