题目内容
一元二次方程a(x+1)2+b(x+1)+c=0化为一般式后为3x2+2x-1=0,试求a2+b2-c2的值的算术平方根.
【答案】分析:把a(x+1)2+b(x+1)+c=0去括号、合并同类项,化作一元二次方程的一般形式,对照3x2+2x-1=0,求出a、b、c的值,再代入计算.
解答:解:整理a(x+1)2+b(x+1)+c=0得ax2+(2a+b)x+(a+b+c)=0,
则 ,
,
解得 ,
,
∴a2+b2-c2=9+16=25,
∴a2+b2-c2的值的算术平方根是5.
点评:此题主要考查一元二次方程的一般形式是:ax2+bx+c=0(a,b,c是常数且a≠0),注意最后的一步是求算术平方根,容易忽略.
解答:解:整理a(x+1)2+b(x+1)+c=0得ax2+(2a+b)x+(a+b+c)=0,
则
 ,
,解得
 ,
,∴a2+b2-c2=9+16=25,
∴a2+b2-c2的值的算术平方根是5.
点评:此题主要考查一元二次方程的一般形式是:ax2+bx+c=0(a,b,c是常数且a≠0),注意最后的一步是求算术平方根,容易忽略.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
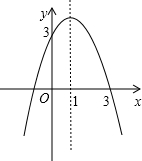 已知二次函数y=-x2+bx+c的图象如图所示,解决下列问题:
已知二次函数y=-x2+bx+c的图象如图所示,解决下列问题: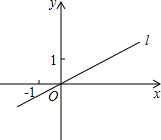 如图,在平面直角坐标系中,直线l的解析式为y=
如图,在平面直角坐标系中,直线l的解析式为y=