题目内容
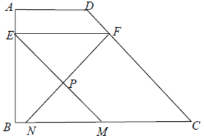
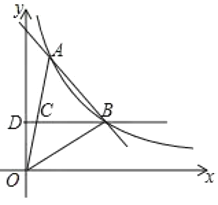
【题目】如图,一次函数y=ax+b与反比例函数y=![]() (x>0)的图像在第一象限交于A、B两点,点B坐标为(4,2),连接OA、OB,过点B作BD⊥y轴,垂足为D,交OA于点C,且OC=CA.
(x>0)的图像在第一象限交于A、B两点,点B坐标为(4,2),连接OA、OB,过点B作BD⊥y轴,垂足为D,交OA于点C,且OC=CA.
(1)求反比例函数和一次函数的表达式;
(2)根据图像直接说出不等式ax+b-![]() <0的解集为______;
<0的解集为______;
(3)求△ABC的面积.
【答案】(1)y=-x+6;y=![]() ;(2)0<x<2或x>4;(3)S△ABC=3.
;(2)0<x<2或x>4;(3)S△ABC=3.
【解析】
(1)此处由题意可先求出反比例函数表达式,再根据CO=CA设出A点坐标求出A点坐标,代入即可求出一次函数表达式.
(2)此处根据数形结合找出一次函数与反比例函数关系即可.
(3)此题可先求出C点坐标,根据A,B,C三点坐标求面积即可.
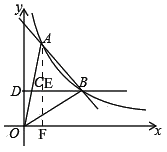
(1)如图,过点A作AF⊥x轴交BD于E,
∵点B(4,2)在反比例函数y=![]() 的图象上,
的图象上,
∴k=4×2=8,
∴反比例函数的表达式为y=![]() ,
,
∵B(4,2),
∴EF=2,
∵BD⊥y轴,OC=CA,
∴AE=EF=![]() AF,
AF,
∴AF=4,
∴点A的纵坐标为4,
∵点A在反比例函数y=![]() 的图象上,
的图象上,
∴A(2,4),
∴4a+b=2;2a+b=4,
∴a=-1 b=6,
∴一次函数的表达式为y=-x+6;
(2)0<x<2或x>4.
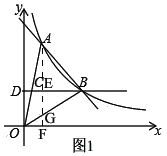
(3)如图1,过点A作AF⊥x轴于F交OB于G,
∵A(2,4),
∴直线OA的解析式为y=2x,
∴C(1,2),
∵A(2,4),
∴AE=4-2=2,BC=4-1=3,
∴S△ABC=![]() ×2×3=3.
×2×3=3.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目