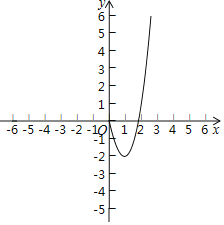题目内容
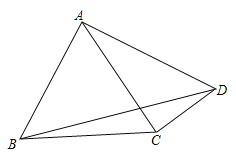
【题目】已知在四边形
中，
，
，连接
，若
，
，则的长度为________.
【答案】
【解析】
根据等边三角形的判定定理得到△ABC是等边三角形，求出∠BAC=60°，过点C作CE⊥AD于E，解直角三角形得到DE=
，求得
，根据直角三角形的性质得到∠CAD=30°，求得∠ACE=60°，∠BAD=90°，得到∠ACD=90°，根据勾股定理即可得到结论．
∵
，
，
∴△ABC是等边三角形，
∴∠BAC=60°，
过点C作CE⊥AD于E，
∴∠AEC=∠CED=90°，
∵∠ADC=60°，
∴∠DCE=30°，
∵CD=2，
∴DE=，
∴，
∵AC=
,
∴CE=
,
∴∠CAD=30°，
∴∠ACE=60°，∠BAD=90°，
∴∠ACD=90°，
∴AD=2CD=4，
∴
.
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
相关题目
【题目】某课外学习小组根据学习函数的经验，对函数y＝x3﹣3x的图象与性质进行了探究．请补充完整以下探索过程：
(1)列表：
x | … | ﹣2 |
| ﹣1 |
| 0 |
| 1 |
| 2 | … |
y | … | ﹣2 | m | 2 |
| 0 |
| n |
| 2 | … |
请直接写出m，n的值；
(2)根据上表中的数据，在平面直角坐标系内补全该函数的图象；
(3)若函数y＝x3﹣3x的图象上有三个点A(x1，y1)，B(x2，y2)，C(x3，y3)，且x1＜﹣2＜x2＜2＜x3，则y1，y2，y3之间的大小关系为 (用“＜”连接)；
(4)若方程x3﹣3x＝k有三个不同的实数根．请根据函数图象，直接写出k的取值范围．
