题目内容
(1)x2-4x-3=0
(2)x2- x-
x- =0
=0
(3)解方程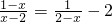
解:(1)x2-4x-3=0,
∵a=1,b=-4,c=-3,
∴x= =
= =
= ,
,
∴x1= ,x2=
,x2=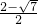 ;
;
(2)x2- x-
x- =0
=0
∵a=1,b=- ,c=-
,c=- ,
,
∴△=b2-4ac=(- )2-4×1×(-
)2-4×1×(- )=3,
)=3,
∴x= ,即x1=
,即x1= ,x2=
,x2= ;
;
(3)由原方程去分母,得
1-x=-1-2(x-2),
移项、合并同类项,得
(-1+2)x=-1+4-1,即x=2,
将x=2代入原方程知,x-2=0,即 无意义,故原方程无解.
无意义,故原方程无解.
分析:(1)、(2)利用求根公式x= 来解方程;
来解方程;
(3)先去分母,将原方程整理为一元一次方程,通过解一元一次方程即可求得x的值.注意,分式方程需要验根.
点评:本题考查了解一元二次方程--公式法,解分式方程.解分式方程时,一定要验根,以防有增根.
∵a=1,b=-4,c=-3,
∴x=
 =
= =
= ,
,∴x1=
 ,x2=
,x2=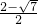 ;
;(2)x2-
 x-
x- =0
=0∵a=1,b=-
 ,c=-
,c=- ,
,∴△=b2-4ac=(-
 )2-4×1×(-
)2-4×1×(- )=3,
)=3,∴x=
 ,即x1=
,即x1= ,x2=
,x2= ;
;(3)由原方程去分母,得
1-x=-1-2(x-2),
移项、合并同类项,得
(-1+2)x=-1+4-1,即x=2,
将x=2代入原方程知,x-2=0,即
 无意义,故原方程无解.
无意义,故原方程无解.分析:(1)、(2)利用求根公式x=
 来解方程;
来解方程;(3)先去分母,将原方程整理为一元一次方程,通过解一元一次方程即可求得x的值.注意,分式方程需要验根.
点评:本题考查了解一元二次方程--公式法,解分式方程.解分式方程时,一定要验根,以防有增根.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
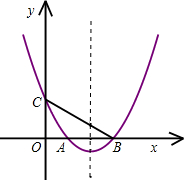 与原抛物线交于点M,当△MA′B′的面积为
与原抛物线交于点M,当△MA′B′的面积为