题目内容
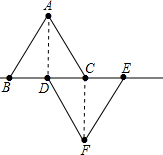
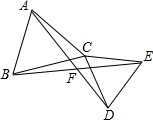 如图,已知△ABC和△CDE都是等边三角形,AD、BE交于点F,则∠AFB等于
如图,已知△ABC和△CDE都是等边三角形,AD、BE交于点F,则∠AFB等于
- A.50°
- B.60°
- C.45°
- D.∠BCD
B
分析:因为△ABC和△CDE都是等边三角形,可证△ACD≌△BCE,所以∠CAD=∠CBE,设AD与BC相交于P点,在△ACG和△BFP中,有一对对顶角,所以∠AFB=∠ACB=60°.
解答: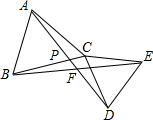 解:∵△ABC和△CDE都是等边三角形,
解:∵△ABC和△CDE都是等边三角形,
∴AC=BC,CE=CD,∠ACB+∠BCD=∠ECD+∠BCD,即∠ACD=∠BCE,
在△ACD和△BCE中,
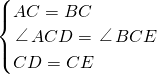 ,
,
∴△ACD≌△BCE(SAS),
∴∠CAD=∠CBE,
设AD与BC相交于P点,在△ACP和△BFP中,有一对对顶角,
∴∠AFB=∠ACB=60°.
故选B.
点评:此题主要考查了等边三角形的性质,有多种解法,也可看做是把△ADC绕C逆时针旋转60°.A落于B,D落于E,AD落于BE,BE由AD旋转60°而得.
分析:因为△ABC和△CDE都是等边三角形,可证△ACD≌△BCE,所以∠CAD=∠CBE,设AD与BC相交于P点,在△ACG和△BFP中,有一对对顶角,所以∠AFB=∠ACB=60°.
解答:
 解:∵△ABC和△CDE都是等边三角形,
解:∵△ABC和△CDE都是等边三角形,∴AC=BC,CE=CD,∠ACB+∠BCD=∠ECD+∠BCD,即∠ACD=∠BCE,
在△ACD和△BCE中,
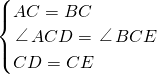 ,
,∴△ACD≌△BCE(SAS),
∴∠CAD=∠CBE,
设AD与BC相交于P点,在△ACP和△BFP中,有一对对顶角,
∴∠AFB=∠ACB=60°.
故选B.
点评:此题主要考查了等边三角形的性质,有多种解法,也可看做是把△ADC绕C逆时针旋转60°.A落于B,D落于E,AD落于BE,BE由AD旋转60°而得.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目

 ,连接AD、CF.
,连接AD、CF. 19、如图,已知△ABC和△A″B″C″及点O.
19、如图,已知△ABC和△A″B″C″及点O. 23、如图,已知△ABC和两条相交于O点且夹角为60°的直线m、n.
23、如图,已知△ABC和两条相交于O点且夹角为60°的直线m、n. (2012•南岗区二模)如图,已知△ABC和△DBE均为等腰直角三角形,∠ABC=∠DBE=90°,求证:AD=CE.
(2012•南岗区二模)如图,已知△ABC和△DBE均为等腰直角三角形,∠ABC=∠DBE=90°,求证:AD=CE.