题目内容
【题目】如图,已知点![]() 分别在线段
分别在线段![]() 上,
上,![]() 交
交![]() 于点
于点![]() 平分
平分![]() .
.
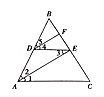
(1)求证:![]() 平分
平分![]() 阅读下列推理过程,并将推理过程补充完整.
阅读下列推理过程,并将推理过程补充完整.
证明:![]() 平分
平分![]() ,(已知)
,(已知)
![]() (角平分线的定义)
(角平分线的定义)
![]() ,(已知)
,(已知)
![]() ( )
( )
故 .(等量代换)
![]() ,(已知)
,(已知)
![]() ,( )
,( )
![]() ,( )
,( )
![]() ,
,
![]() 平分
平分![]() .( )
.( )
(2)若![]() ,请直接写出图中所有与
,请直接写出图中所有与![]() 互余的角.
互余的角.
【答案】(1)![]() ;两直线平行,内错角相等;
;两直线平行,内错角相等;![]() ;两直线平行,同位角相等;两直线平行,内错角相等;角平分线的定义;(2)
;两直线平行,同位角相等;两直线平行,内错角相等;角平分线的定义;(2)![]() 和
和![]()
【解析】
(1)根据角平分线的定义得到∠1=∠2,根据平行线的性质得到∠1=∠3,等量代换得到∠2=∠3,根据平行线的性质得到∠2=∠5,等量代换即可得到结论;
(2)根据垂直的定义得到∠3+∠DEB=90°,∠1+∠C=90°,由平行线的性质得出∠5+∠B=90°,然后由∠3=∠1=∠4=∠5得出与∠1互余的角.
解:(1)![]() 平分
平分![]() ,(已知)
,(已知)
![]() (角平分线的定义)
(角平分线的定义)
![]() ,(已知)
,(已知)
![]() ,(两直线平行,内错角相等)
,(两直线平行,内错角相等)
故![]() (等量代换)
(等量代换)
![]() ,(已知)
,(已知)
![]() ,(两直线平行,同位角相等)
,(两直线平行,同位角相等)
![]() ,(两直线平行,内错角相等)
,(两直线平行,内错角相等)
![]() ,(等量代换)
,(等量代换)
![]() 平分
平分![]() .(角平分线的定义)
.(角平分线的定义)
故答案为:![]() ;两直线平行,内错角相等;
;两直线平行,内错角相等;![]() ;两直线平行,同位角相等;两直线平行,内错角相等;角平分线的定义;
;两直线平行,同位角相等;两直线平行,内错角相等;角平分线的定义;
(2)∵![]() ,
,![]()
∴∠AEB=∠DFB=90°
∴∠3+∠DEB=90°,∠1+∠C=90°,∠5+∠B=90°,
又由①可知∠3=∠1=∠4=∠5
∴∠1+∠DEB=90°,∠1+∠B=90°,
∴与![]() 互余的角有
互余的角有![]() 和
和![]() .
.

练习册系列答案
相关题目