题目内容
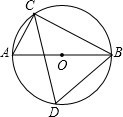
 如图,在⊙O中,直径AB与弦CD相交于点P,
如图,在⊙O中,直径AB与弦CD相交于点P, =92°,
=92°, =46°
=46°
(1)求∠BPD的度数;
(2)求证:OC•BP=OP•BD.
解:(1)∵ =92°,
=92°, =46°,
=46°,
∴∠PBD=46°,∠PDB=23°,
∴∠BPD=180°-46°-23°=111°.
(2)证明: 的度数为46°,
的度数为46°,
∴∠POC=46°,
在△OPC和△BPD中,∵∠POC=∠PBD=46°,∠OPC=∠BPD,
∴△OPC∽△BPD,
∴ =
=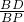 ,
,
即OC•BP=OP•BD.
分析:(1)先求出∠PBD及∠PDB的度数,继而在△PBD中利用三角形的内角和定理可得出∠BPD的度数;
(2)先确定∠POC=46°,然后可判定△OPC∽△BPD,利用相似三角形的性质可得出结论.
点评:本题考查了圆周角定理、相似三角形的判定与性质,解答本题的关键是掌握各个定理的内容.
 =92°,
=92°, =46°,
=46°,∴∠PBD=46°,∠PDB=23°,
∴∠BPD=180°-46°-23°=111°.
(2)证明:
 的度数为46°,
的度数为46°,∴∠POC=46°,
在△OPC和△BPD中,∵∠POC=∠PBD=46°,∠OPC=∠BPD,
∴△OPC∽△BPD,
∴
 =
=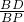 ,
,即OC•BP=OP•BD.
分析:(1)先求出∠PBD及∠PDB的度数,继而在△PBD中利用三角形的内角和定理可得出∠BPD的度数;
(2)先确定∠POC=46°,然后可判定△OPC∽△BPD,利用相似三角形的性质可得出结论.
点评:本题考查了圆周角定理、相似三角形的判定与性质,解答本题的关键是掌握各个定理的内容.

练习册系列答案
相关题目
 如图,在⊙O中,直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,则BC=
如图,在⊙O中,直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,则BC=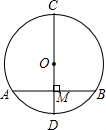 如图,在⊙O中,直径CD的长度为10cm,AB是弦,且AB⊥CD于M,OM=3cm,求弦AB的长.
如图,在⊙O中,直径CD的长度为10cm,AB是弦,且AB⊥CD于M,OM=3cm,求弦AB的长.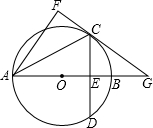 C与直线AB相交于点G.
C与直线AB相交于点G. (2013•百色)如图,在⊙O中,直径CD垂直于弦AB,若∠C=25°,则∠ABO的度数是( )
(2013•百色)如图,在⊙O中,直径CD垂直于弦AB,若∠C=25°,则∠ABO的度数是( ) (2012•朝阳区二模)如图,在⊙O中,直径AB⊥弦CD于点H,E是⊙O上的点,若∠BEC=25°,则∠BAD的度数为( )
(2012•朝阳区二模)如图,在⊙O中,直径AB⊥弦CD于点H,E是⊙O上的点,若∠BEC=25°,则∠BAD的度数为( )