题目内容
 (2012•贵阳)如图,二次函数y=
(2012•贵阳)如图,二次函数y=| 1 |
| 2 |
(1)若A(-4,0),求二次函数的关系式;
(2)在(1)的条件下,求四边形AMBM′的面积;
(3)是否存在抛物线y=
| 1 |
| 2 |
分析:(1)把点A的坐标代入二次函数解析式,计算求出c的值,即可得解;
(2)把二次函数解析式整理成顶点式解析式,根据二次函数的对称性求出点B的坐标,从而求出AB的长,再根据顶点坐标求出点M到x轴的距离,然后求出△ABM的面积,根据对称性可得S四边形AMBM′=2S△ABM,计算即可得解;
(3)令y=0,得到关于x的一元二次方程,利用根与系数的关系求出AB的长度,根据抛物线解析式求出顶点M的纵坐标,然后根据正方形的对角线互相垂直平分且相等列式求解,如果关于c的方程有解,则存在,否则不存在.
(2)把二次函数解析式整理成顶点式解析式,根据二次函数的对称性求出点B的坐标,从而求出AB的长,再根据顶点坐标求出点M到x轴的距离,然后求出△ABM的面积,根据对称性可得S四边形AMBM′=2S△ABM,计算即可得解;
(3)令y=0,得到关于x的一元二次方程,利用根与系数的关系求出AB的长度,根据抛物线解析式求出顶点M的纵坐标,然后根据正方形的对角线互相垂直平分且相等列式求解,如果关于c的方程有解,则存在,否则不存在.
解答:解:(1)∵A(-4,0)在二次函数y=
x2-x+c的图象上,
∴
×(-4)2-(-4)+c=0,
解得c=-12,
∴二次函数的关系式为y=
x2-x-12;
(2)∵y=
x2-x-12,
=
(x2-2x+1)-
-12,
=
(x-1)2-
,
∴顶点M的坐标为(1,-
),
∵A(-4,0),对称轴为x=1,
∴点B的坐标为(6,0),
∴AB=6-(-4)=6+4=10,
∴S△ABM=
×10×
=
,
∵顶点M关于x轴的对称点是M′,
∴S四边形AMBM′=2S△ABM=2×
=125;
(3)存在抛物线y=
x2-x-
,使得四边形AMBM′为正方形.
理由如下:令y=0,则
x2-x+c=0,设点AB的坐标分别为A(x1,0)B(x2,0),
则x1+x2=-
=2,x1•x2=
=2c,
所以,AB=
=
,
点M的纵坐标为:
=
=
,
∵顶点M关于x轴的对称点是M′,四边形AMBM′为正方形,
∴
=2×
,
整理得,4c2+4c-3=0,
解得c1=
,c2=-
,
又抛物线与x轴有两个交点,
∴△=b2-4ac=(-1)2-4×
c>0,
解得c<
,
∴c的值为-
,
故存在抛物线y=
x2-x-
,使得四边形AMBM′为正方形.
| 1 |
| 2 |
∴
| 1 |
| 2 |
解得c=-12,
∴二次函数的关系式为y=
| 1 |
| 2 |
(2)∵y=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 25 |
| 2 |

∴顶点M的坐标为(1,-
| 25 |
| 2 |
∵A(-4,0),对称轴为x=1,
∴点B的坐标为(6,0),
∴AB=6-(-4)=6+4=10,
∴S△ABM=
| 1 |
| 2 |
| 25 |
| 2 |
| 125 |
| 2 |
∵顶点M关于x轴的对称点是M′,
∴S四边形AMBM′=2S△ABM=2×
| 125 |
| 2 |
(3)存在抛物线y=
| 1 |
| 2 |
| 3 |
| 2 |
理由如下:令y=0,则
| 1 |
| 2 |
则x1+x2=-
| -1 | ||
|
| c | ||
|
所以,AB=
| (x1+x2)2-4x1x2 |
| 4-8c |

点M的纵坐标为:
| 4ac-b2 |
| 4a |
4×
| ||
4×
|
| 2c-1 |
| 2 |
∵顶点M关于x轴的对称点是M′,四边形AMBM′为正方形,
∴
| 4-8c |
| 1-2c |
| 2 |
整理得,4c2+4c-3=0,
解得c1=
| 1 |
| 2 |
| 3 |
| 2 |
又抛物线与x轴有两个交点,
∴△=b2-4ac=(-1)2-4×
| 1 |
| 2 |
解得c<
| 1 |
| 2 |
∴c的值为-
| 3 |
| 2 |
故存在抛物线y=
| 1 |
| 2 |
| 3 |
| 2 |
点评:本题综合考查了二次函数的问题,主要利用了待定系数法求函二次数解析式,二次函数的顶点坐标的求解,二次函数的对称性,以及正方形的对角线互相垂直平分且相等的性质,综合题,但难度不是很大,(3)中要注意根据抛物线与x轴有两个交点,利用根的判别式求出c的取值范围,否则容易多解而导致出错.

练习册系列答案
相关题目
 (2012•贵阳)如图,已知点A、D、C、F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是( )
(2012•贵阳)如图,已知点A、D、C、F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是( )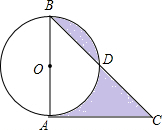 (2012•贵阳)如图,在⊙O中,直径AB=2,CA切⊙O于A,BC交⊙O于D,若∠C=45°,则
(2012•贵阳)如图,在⊙O中,直径AB=2,CA切⊙O于A,BC交⊙O于D,若∠C=45°,则 (2012•贵阳)如图,在△ABA1中,∠B=20°,AB=A1B,在A1B上取一点C,延长AA1到A2,使得A1A2=A1C;在A2C上取一点D,延长A1A2到A3,使得A2A3=A2D;…,按此做法进行下去,∠An的度数为
(2012•贵阳)如图,在△ABA1中,∠B=20°,AB=A1B,在A1B上取一点C,延长AA1到A2,使得A1A2=A1C;在A2C上取一点D,延长A1A2到A3,使得A2A3=A2D;…,按此做法进行下去,∠An的度数为 (2012•贵阳)如图,一次函数y=k1x+b1的图象l1与y=k2x+b2的图象l2相交于点P,则方程组
(2012•贵阳)如图,一次函数y=k1x+b1的图象l1与y=k2x+b2的图象l2相交于点P,则方程组 (2012•贵阳)如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交于BC的延长线于F,若∠F=30°,DE=1,则EF的长是( )
(2012•贵阳)如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交于BC的延长线于F,若∠F=30°,DE=1,则EF的长是( )