题目内容

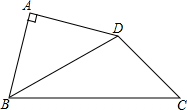如图，四边形ABCD中，AB=AD，∠BAD=90°，∠CBD=30°，∠BCD=45°，若AB=2 $数学公式$ ．求四边形ABCD的面积．

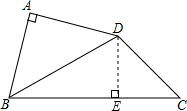解：如图，过点D作DE⊥BC于E，
∵AB=AD，∠BAD=90°，
∴AD=AB=2 $\text{[math]}$ ，
BD=2 $\text{[math]}$ × $\text{[math]}$ =4，
∵∠CBD=30°，
∴DE= $\text{[math]}$ BD= $\text{[math]}$ ×4=2，
BE= $\text{[math]}$ = $\text{[math]}$ =2 $\text{[math]}$ ，
∵∠BCD=45°，
∴CE=DE=2，
∴BC=BE+CE=2 $\text{[math]}$ +2，
∴四边形ABCD的面积=S_△ABD+S_△BCD= $\text{[math]}$ ×2 $\text{[math]}$ ×2 $\text{[math]}$ + $\text{[math]}$ ×（2 $\text{[math]}$ +2）×2，
=4+2 $\text{[math]}$ +2，
=2 $\text{[math]}$ +6．
分析：过点D作DE⊥BC于E，根据等腰直角三角形的性质求出AD、BD，再根据直角三角形30°角所对的直角边等于斜边的一半求出DE，利用勾股定理列式求出BE，判断出△CDE是等腰直角三角形，然后求出CE的长，再根据三角形的面积公式列式进行计算即可得解．
点评：本题考查了勾股定理，直角三角形30°角所对的直角边等于斜边的一半的性质，等腰直角三角形的性质，作辅助线，把△BCD分成两个直角三角形是解题的关键，也是本题的难点．