题目内容
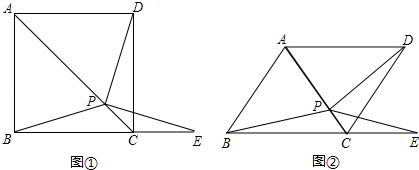
正方形ABCD中,AC、BD相交于点O,点E是射线AB上一点,点F是直线AD上一点,BE=DF,连接EF交线段BD于点G,交AO于点H.若AB=3,AG= ,则线段EH的长为 .
,则线段EH的长为 .
 ,则线段EH的长为 .
,则线段EH的长为 . 或
或
试题分析:由EF与线段BD相交,可知点E、F位于直线BD的两侧,因此有两种情形:
①点E在线段AB上,点F在线段AD延长线上,依题意画出图形,如图所示:

过点E作EM⊥AB,交BD于点M,则EM∥AF,△BEM为等腰直角三角形,
∵EM∥AF,∴∠EMG=∠FDG,∠GEM=∠F。
∵△BEM为等腰直角三角形,∴EM=BE。
∵BE=DF,∴EM=DF。
∵在△EMG与△FDG中,EM=DF,∠EMG=∠FDG,∠GEM=∠F,
∴△EMG≌△FDG(ASA)。
∴EG=FG,即G为EF的中点。
∴EF=2AG=2
 (直角三角形斜边上的中线长等于斜边长的一半)。
(直角三角形斜边上的中线长等于斜边长的一半)。设BE=DF=x,则AE=3﹣x,AF=3+x,
在Rt△AEF中,由勾股定理得:AE2+AF2=EF2,即(3﹣x)2+(3+x)2=(2
 )2。
)2。解得x=1,即BE=DF=1。∴AE=2,AF=4。∴tan∠F=
 。
。设EF与CD交于点K,则在Rt△DFK中,DK=DF•tan∠F=
 ,
,∴CK=CD﹣DK=
 。
。∵AB∥CD,∴△AEH≌△CKH,∴
 。
。∵AC=AH+CH=3
 ,∴AH=
,∴AH= AC=
AC= 。
。过点H作HN∥AE,交AD于点N,则△ANH为等腰直角三角形,
∴AN=
 AH=
AH= 。
。∵HN∥AE,∴
 ,即
,即 。∴EH=
。∴EH= 。
。②点E在线段AB的延长线上,点F在线段AD上,依题意画出图形,如图所示,

同理可求得:EH=
 。
。综上所述,线段EH的长为
 或
或 。
。
练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目


 BD
BD