题目内容
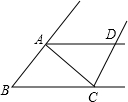
 如图,△ABC≌△ADE,∠B=30°,∠E=30°,∠BAE=80°,求∠BAC、∠DAC的度数.
如图,△ABC≌△ADE,∠B=30°,∠E=30°,∠BAE=80°,求∠BAC、∠DAC的度数.分析:根据全等三角形对应角相等可得∠C=∠E,再根据三角形的内角和定理列式计算即可求出∠BAC,先求出∠CAE,再根据全等三角形对应角相等可得∠DAE=∠BAC,然后根据∠DAC=∠DAE+∠CAE代入数据计算即可得解.
解答:解:∵△ABC≌△ADE,
∴∠C=∠E=20°,
在△ABC中,∠BAC=180°-∠B-∠C=180°-30°-20°=130°;
∵∠BAE=80°,
∴∠CAE=∠BAC-∠BAE=130°-80°=50°,
∵△ABC≌△ADE,
∴∠DAE=∠BAC=130°,
∴∠DAC=∠DAE+∠CAE=130°+50°=180°.
故,∠BAC=130°,∠DAC=180°.
∴∠C=∠E=20°,
在△ABC中,∠BAC=180°-∠B-∠C=180°-30°-20°=130°;
∵∠BAE=80°,
∴∠CAE=∠BAC-∠BAE=130°-80°=50°,
∵△ABC≌△ADE,
∴∠DAE=∠BAC=130°,
∴∠DAC=∠DAE+∠CAE=130°+50°=180°.
故,∠BAC=130°,∠DAC=180°.
点评:本题考查了全等三角形对应角相等的性质,三角形的内角和定理,熟记性质并准确识图,理清图中各角度之间的关系是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
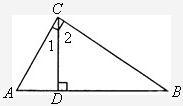
 如图,△ABC的两个外角的平分线相交于D,若∠B=50°,则∠ADC=( )
如图,△ABC的两个外角的平分线相交于D,若∠B=50°,则∠ADC=( )| A、60° | B、80° | C、65° | D、40° |
 ,且CB=CE.
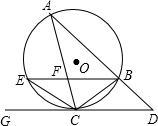
,且CB=CE. 5、已知:如图,△ABC内接于⊙O,AE切⊙O于点A,BD∥AE交AC的延长线于点D,求证:AB2=AC•AD.
5、已知:如图,△ABC内接于⊙O,AE切⊙O于点A,BD∥AE交AC的延长线于点D,求证:AB2=AC•AD.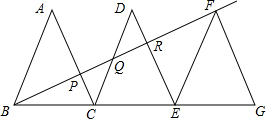 如图,△ABC、△DCE、△FEG是全等的三个等腰三角形,底边BC、CE、EG在同一直线上,且
如图,△ABC、△DCE、△FEG是全等的三个等腰三角形,底边BC、CE、EG在同一直线上,且