题目内容
(本题8分)
如图,矩形ABCD内接于⊙O,且AB=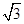 ,BC=1,求图中阴影部分所表示的扇形OAD的面积.
,BC=1,求图中阴影部分所表示的扇形OAD的面积. 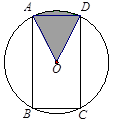
S扇形OAD=
解析 试题分析:∵矩形ABCD内接于⊙O,∴∠B=90o,连结AC。
试题分析:∵矩形ABCD内接于⊙O,∴∠B=90o,连结AC。
∴AC是直径,AC过点O.
Rt△ABC中,AB=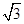 ,BC=1,
,BC=1,
∴,通过勾股定理求出AC=2,扇形OAD的半径R= ="1" ,又∵sin∠BAC=
="1" ,又∵sin∠BAC= ,
,
∴∠BAC=30o,∵AB//DC,∴∠ACD=30o,∴∠AOD=2∠ACD =60o
S扇形OAD=
考点:圆心角与圆周角之间的关系转化
点评:难度较低。本题考查学生对圆心角与圆周角之间的关系转化,通过转化为求圆周角的角度,转化成求直角三角形中其中一个角的角度。利用直角边的边长求正弦值来求角的大小。最后利用扇形面积公式求出答案。学习几何问题后,要能够熟悉各几何图形的各方面计算公式。

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
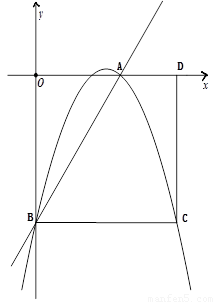
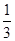 x2+bx+c经过点A、B,请求出这条抛物线的解析式;
x2+bx+c经过点A、B,请求出这条抛物线的解析式;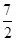 ≤x≤7,在抛物线上存在点P,使△ABP的面积最大,那么△ABP最大面积是 .(请直接写出结论,不需要写过程)
≤x≤7,在抛物线上存在点P,使△ABP的面积最大,那么△ABP最大面积是 .(请直接写出结论,不需要写过程) 内接于⊙O,点
内接于⊙O,点 在半径
在半径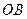 的延长线上,
的延长线上,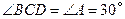 .
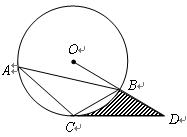
.
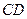 与⊙O的位置关系,并说明理由;
与⊙O的位置关系,并说明理由;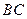 、线段
、线段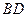 所围成的阴影部分面积(结果保留
所围成的阴影部分面积(结果保留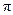 和根号).
和根号).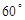 后的对应点为点C.
后的对应点为点C.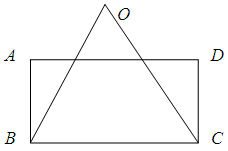
 x2+bx+c经过点A、B,请求出这条抛物线的解析式;
x2+bx+c经过点A、B,请求出这条抛物线的解析式;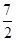 ≤x≤7,在抛物线上存在点P,使△ABP的面积最大,那么△ABP最大面积是 .(请直接写出结论,不需要写过程)
≤x≤7,在抛物线上存在点P,使△ABP的面积最大,那么△ABP最大面积是 .(请直接写出结论,不需要写过程)