题目内容
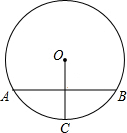 如图,⊙O的弦AB垂直平分半径OC,若AB=
如图,⊙O的弦AB垂直平分半径OC,若AB= ,则⊙O的半径为________.
,则⊙O的半径为________.

分析:连OA,AB交OC于D点,设半径为R,由AB垂直平分半径OC,根据垂径定理得到DA=DB=
 AB=
AB= ,且有OD=
,且有OD= OC,在Rt△AOD中,OD=
OC,在Rt△AOD中,OD= R,利用勾股定理可得到R2=(
R,利用勾股定理可得到R2=( )2+(
)2+( R)2,即可求出R=
R)2,即可求出R= .
.解答:连OA,AB交OC于D点,如图
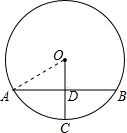 ,
,设半径为R,
∵AB垂直平分半径OC,
∴DA=DB,OD=
 OC,
OC,而AB=
 ,
,∴AD=
 ,
,在Rt△AOD中,OD=
 R,
R,∵OA2=AD2+OD2,即R2=(
 )2+(
)2+( R)2,
R)2,∴R=
 .
.故答案为
 .
.点评:本题考查了垂径定理:垂直于弦的直径平分弦,并且平分弦所对的弧.也考查了勾股定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

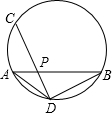





 ,即可得到OC,AB
,即可得到OC,AB
 OP,则OP=
OP,则OP=