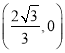题目内容
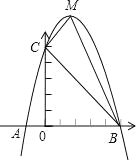
【题目】如图,直线y=x+4与两坐标轴相交于A,B两点,点P为线段OA上的动点,连结BP,过点A作AM垂直于直线BP,垂足为M,当点P从点O运动到点A时,则点M经过的路径长为_____.
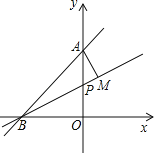
【答案】![]() π.
π.
【解析】
根据直线与两坐标轴交点坐标的特点可得A、B两点坐标,由题意可得点M的路径是以AB的中点N为圆心,AB长的一半为半径的弧OA,求出弧OA的长度即可得出结果.
解:∵AM垂直于直线BP,
∴∠BMA=90°,
∴点M的路径是以AB的中点N为圆心,![]() AB长为半径的弧OA,
AB长为半径的弧OA,
连接ON,如图所示:
∵直线y=x+4与两坐标轴交A、B两点,
∴OA=OB=4,
∴ON⊥AB,
∴∠ONA=90°,
∵AB=![]() =
=![]() =4
=4![]() ,
,
∴ON=![]() AB=2
AB=2![]() ,
,
∴点M经过的路径长=![]() ×2
×2![]() =
=![]() π,
π,
故答案为:![]() π.
π.


练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目