��Ŀ����
��֪������y=ax2-��a+c��x+c������a��c��a��0����
��1�������������x��Ľ������ꣻ����a��c�Ĵ���ʽ��ʾ��
��2���������������߶���A��ֱ��y=-x+k��������ߵ���һ������ΪB��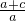 ��-c������������ߵĽ���ʽ��
��-c������������ߵĽ���ʽ��
��3����P�ڣ�2����x���Ϸ����������ϣ�ֱ��y=-x+k�� y��Ľ���ΪC����tan��POB= tan��POC�����P�����ꣻ
tan��POC�����P�����ꣻ
��4������2���еĶ��κ������Ա���x��n��x��n+1��nΪ���������ķ�Χ��ȡֵʱ����������������ֵ�ĸ���ΪN����N����n�ĺ�����ϵʽΪ______��
�⣺��1��������y=ax2-��a+c��x+c��x�ύ��ĺ������ǹ���x�ķ���ax2-��a+c��x+c=0������a��0��a��c���Ľ⣮
���x1=1��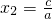 ��
��
����������x�ύ�������Ϊ��1��0����
��2��������y=ax2-��a+c��x+c�Ķ���A������Ϊ ��
��
�߾����������߶���A��ֱ��y=-x+k��������ߵ���һ������Ϊ ��
��
��
�ɢ۵�c=0��
�������١��ڵ�
���a=-2��
�����������ߵĽ���ʽΪy=-2x2+2x��
��3����PE��x���ڵ�E��PF��y���ڵ�F������ͼ��
 ������y=-2x2+2x�Ķ���A������
������y=-2x2+2x�Ķ���A������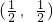 ��
��
��B��������1��0������C��������0��1����
���P��������m��n����
�ߵ�P��x���Ϸ���������y=-2x2+2x�ϣ�
��n=-2m2+2m����0��m��1�� ��
��
�� ��
�� ��
��
�� ��
��
��m2=4n2��
���m=2n����m=-2n����ȥ����
��m=2n����n=-2m2+2m����8n2-3n=0��
��� ��n2=0����ȥ����
��n2=0����ȥ����
�� ��
��
���P������Ϊ ��
��
��4��N����n�ĺ�����ϵʽΪN=4n��
˵�������κ���y=-2x2+2x���Ա���x��n��x��n+1��nΪ���������ķ�Χ��ȡֵ����ʱy��x���������С��
��-2n2-2n��y��-2n2+2n��
���������-2n2-2n+1��-2n2-2n+2��-2n2+2n��N=��-2n2+2n��-��-2n2-2n��=4n��
��������1�����ö��κ�����x���ཻy=0�����ɽ����
��2�����ȱ�ʾ�����κ����Ķ������꣬���ô���ϵ���������
��3����PE��x���ڵ�E��PF��y���ڵ�F���������Ǻ�����ϵ�����
��4�������Ա�����ȡֵ��Χ��������κ�������ʽ�����ɽ����
������������Ҫ�����˶��κ�����x��Ľ������꣬�Լ����κ�����������ı�ʾ���������κ�������ʽ���ȣ��ۺ��ԱȽ�ǿ��
���x1=1��
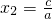 ��
������������x�ύ�������Ϊ��1��0����

��2��������y=ax2-��a+c��x+c�Ķ���A������Ϊ
 ��
���߾����������߶���A��ֱ��y=-x+k��������ߵ���һ������Ϊ
 ��
����

�ɢ۵�c=0��
�������١��ڵ�

���a=-2��
�����������ߵĽ���ʽΪy=-2x2+2x��
��3����PE��x���ڵ�E��PF��y���ڵ�F������ͼ��
 ������y=-2x2+2x�Ķ���A������
������y=-2x2+2x�Ķ���A������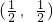 ��
����B��������1��0������C��������0��1����
���P��������m��n����
�ߵ�P��x���Ϸ���������y=-2x2+2x�ϣ�
��n=-2m2+2m����0��m��1��
 ��
����
 ��
�� ��
����
 ��
����m2=4n2��
���m=2n����m=-2n����ȥ����
��m=2n����n=-2m2+2m����8n2-3n=0��
���
 ��n2=0����ȥ����
��n2=0����ȥ������
 ��
�����P������Ϊ
 ��
����4��N����n�ĺ�����ϵʽΪN=4n��
˵�������κ���y=-2x2+2x���Ա���x��n��x��n+1��nΪ���������ķ�Χ��ȡֵ����ʱy��x���������С��
��-2n2-2n��y��-2n2+2n��
���������-2n2-2n+1��-2n2-2n+2��-2n2+2n��N=��-2n2+2n��-��-2n2-2n��=4n��
��������1�����ö��κ�����x���ཻy=0�����ɽ����
��2�����ȱ�ʾ�����κ����Ķ������꣬���ô���ϵ���������
��3����PE��x���ڵ�E��PF��y���ڵ�F���������Ǻ�����ϵ�����
��4�������Ա�����ȡֵ��Χ��������κ�������ʽ�����ɽ����
������������Ҫ�����˶��κ�����x��Ľ������꣬�Լ����κ�����������ı�ʾ���������κ�������ʽ���ȣ��ۺ��ԱȽ�ǿ��

��ϰ��ϵ�д�
�����Ŀ
 ��x�����һ������ΪE��
��x�����һ������ΪE�� ��ͼ����֪������y=ax2+bx+c������b��0��c��0���Ķ���P��x���ϣ���y�ύ�ڵ�Q��������ԭ��O����OA��PQ������ΪA����OA=
��ͼ����֪������y=ax2+bx+c������b��0��c��0���Ķ���P��x���ϣ���y�ύ�ڵ�Q��������ԭ��O����OA��PQ������ΪA����OA=