Question

如图，平面直角坐标系中有一直角梯形OMNH，点H的坐标为（－8，0），点N的坐标为（－6，－4）．

（1）画出直角梯形OMNH绕点O旋转180°的图形OABC，并写出顶点A，B，C的坐标（点M的对应点为A， 点N的对应点为B， 点H的对应点为C）；

（2）求出过A，B，C三点的抛物线的表达式；

（3）截取CE=OF=AG=m，且E，F，G分别在线段CO，OA，AB上，求四边形BEFG的面积S与m之间的函数关系式，并写出自变量m的取值范围；面积S是否存在最小值?若存在，请求出这个最小值；若不存在，请说明理由；

    （4）在（3）的情况下，四边形BEFG是否存在邻边相等的情况，若存在，请直接写出此时m的值，并指出相等的邻边；若不存在，说明理由．

 

Answer 1

解：（1） 利用中心对称性质，画出梯形OABC． ·············· 1分

∵A，B，C三点与M，N，H分别关于点O中心对称，

∴A（0，4），B（6，4），C（8，0）  3分

（写错一个点的坐标扣1分）

（2）设过A，B，C三点的抛物线关系式为，

∵抛物线过点A（0，4），

∴．则抛物线关系式为． 4分

将B（6，4）， C（8，0）两点坐标代入关系式，得

   5分

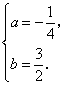解得  6分

所求抛物线关系式为：．··············· 7分

（3）∵OA=4，OC=8，∴AF=4－m，OE=8－m． ················ 8分

     ∴   

                 OA（AB+OC）AF·AGOE·OFCE·OA

                

                   （ 0＜＜4） ············· 10分

∵． ∴当时，S的取最小值．

又∵0＜m＜4，∴不存在m值，使S的取得最小值． ············ 12分

（4）当时，GB=GF，当时，BE=BG．··········· 14分