题目内容
 (1)如图,已知AB=AC,AD=AE,∠BAC=∠CAD=60°,点B、A、E在一条直线上.请判断BD与CE是否相等?并说明理由.
(1)如图,已知AB=AC,AD=AE,∠BAC=∠CAD=60°,点B、A、E在一条直线上.请判断BD与CE是否相等?并说明理由.(2)如果改为:“已知AB=AC,AD=AE,∠BAC=∠EAD,点B、A、E在一条直线上,则BD与CE是否相等?”你会解吗?
分析:(1)、(2)通过证△BAD≌△CAE(SAS)可以得到BD=CE.
解答:解:(1)BD与CE相等,理由如下:
如图,∵∠BAC=∠CAD=60°,点B、A、E在一条直线上,
∴∠DAE=180°-∠BAC-∠CAD=60°,
∴∠BAD=∠CAE=120°,
在△BAD与△CAE中,
,
∴△BAD≌△CAE(SAS),
∴BD=CE;
(2)BD与CE相等,理由如下:
如图,∵∠BAC=∠EAD,点B、A、E在一条直线上,
∴∠BAC+∠CAD=∠EAD+∠CAD,
∴∠BAD=∠CAE,
在△BAD与△CAE中,
,
∴△BAD≌△CAE(SAS),
∴BD=CE.
如图,∵∠BAC=∠CAD=60°,点B、A、E在一条直线上,

∴∠DAE=180°-∠BAC-∠CAD=60°,
∴∠BAD=∠CAE=120°,
在△BAD与△CAE中,
|
∴△BAD≌△CAE(SAS),
∴BD=CE;
(2)BD与CE相等,理由如下:
如图,∵∠BAC=∠EAD,点B、A、E在一条直线上,
∴∠BAC+∠CAD=∠EAD+∠CAD,
∴∠BAD=∠CAE,
在△BAD与△CAE中,
|
∴△BAD≌△CAE(SAS),
∴BD=CE.
点评:本题考查了全等三角形的判定与性质.全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
 24、如图,已知AB=AC,∠1=∠2,∠3=∠F,试判断EC与DF是否平行,并说明理由.
24、如图,已知AB=AC,∠1=∠2,∠3=∠F,试判断EC与DF是否平行,并说明理由. 17、(保留作图痕迹)如图,已知AB=DC.
17、(保留作图痕迹)如图,已知AB=DC.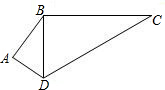 如图,已知AB=4,BC=12,CD=13,DA=3,AB⊥AD.判断BC⊥BD吗?简述你的理由.
如图,已知AB=4,BC=12,CD=13,DA=3,AB⊥AD.判断BC⊥BD吗?简述你的理由. 如图:已知AB∥DE,点C是AE的中点,
如图:已知AB∥DE,点C是AE的中点, 如图,已知AB、CD交于点O,且点O是AB的中点,AC∥BD,请说明点O是CD的中点的理由.
如图,已知AB、CD交于点O,且点O是AB的中点,AC∥BD,请说明点O是CD的中点的理由.