题目内容
 在等腰梯形ABCD中,AD∥BC,对角线AC⊥BD于点O,AE⊥BC,DF⊥BC,垂足分别为E,F,AD=4,BC=8,则AE+EF=
在等腰梯形ABCD中,AD∥BC,对角线AC⊥BD于点O,AE⊥BC,DF⊥BC,垂足分别为E,F,AD=4,BC=8,则AE+EF=
- A.9
- B.10
- C.11
- D.20
B
分析:先根据题意作出辅助线:延长BC至G,使DG∥AC,由AD∥BC,可知四边形ADGC为平行四边形,得出DG=AC,而等腰梯形中两对角线相等,得出DG=BD,而DF⊥BG,则△AEC为等腰直角三角形,从而得到FC=FG-AD=2,则EF=BC-2FC=8-2FC=4,得出AE+EF的值.
解答: 解:过D点作AC的平行线,交BC的延长线于G点,
解:过D点作AC的平行线,交BC的延长线于G点,
∵AD∥BC,
∴四边形ADGC为平行四边形,
∴DG=AC,
∵AC⊥BD,
∴DG⊥BD,
∵等腰梯形ABCD,
∴AC=BD,
∴DG=BD,
∴△DBG为等腰直角三角形,
∴∠G=∠ACE=45°,
∴AE=CE=6,
∴FC=6-4=2,
∴EF=BC-2FC=8-2FC=4,
∴AE+EF=6+4=10.
故选B.
点评:此题考查了等腰梯形的性质,关键是作辅助线,然后利用等腰梯形的性质和等腰直角三角形求解.
分析:先根据题意作出辅助线:延长BC至G,使DG∥AC,由AD∥BC,可知四边形ADGC为平行四边形,得出DG=AC,而等腰梯形中两对角线相等,得出DG=BD,而DF⊥BG,则△AEC为等腰直角三角形,从而得到FC=FG-AD=2,则EF=BC-2FC=8-2FC=4,得出AE+EF的值.
解答:
 解:过D点作AC的平行线,交BC的延长线于G点,
解:过D点作AC的平行线,交BC的延长线于G点,∵AD∥BC,
∴四边形ADGC为平行四边形,
∴DG=AC,
∵AC⊥BD,
∴DG⊥BD,
∵等腰梯形ABCD,
∴AC=BD,
∴DG=BD,
∴△DBG为等腰直角三角形,
∴∠G=∠ACE=45°,
∴AE=CE=6,
∴FC=6-4=2,
∴EF=BC-2FC=8-2FC=4,
∴AE+EF=6+4=10.
故选B.
点评:此题考查了等腰梯形的性质,关键是作辅助线,然后利用等腰梯形的性质和等腰直角三角形求解.

练习册系列答案
相关题目
 25、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,点P为BC边上任意一点,且
25、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,点P为BC边上任意一点,且 24、已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,点E为边BC上一点,且AE=DC.
24、已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,点E为边BC上一点,且AE=DC.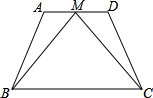 如图,在等腰梯形ABCD中,AD∥BC,M是AD的中点,MB=MC吗?为什么?
如图,在等腰梯形ABCD中,AD∥BC,M是AD的中点,MB=MC吗?为什么? 如图,在等腰梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,垂足为O,过D作DE∥AC交BC的延长线于E.
如图,在等腰梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,垂足为O,过D作DE∥AC交BC的延长线于E.