题目内容
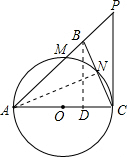
如图,在△ABC中,∠ABC=∠ACB,以AC为直径的⊙O分别交AB、BC于点M、N,点P在AB的延长线上,且∠CAB=2∠BCP.
(1)求证:直线CP是⊙O的切线;
(2)若BC=2
,sin∠BCP=
,求⊙O的半径及△ACP的周长.

(1)求证:直线CP是⊙O的切线;
(2)若BC=2
| 5 |
| ||
| 5 |

(1)证明:连接AN,
∵∠ABC=∠ACB,∴AB=AC,
∵AC是⊙O的直径,∴AN⊥BC,
∴∠CAN=∠BAN,BN=CN,
∵∠CAB=2∠BCP,
∴∠CAN=∠BCP.
∵∠CAN+∠ACN=90°,
∴∠BCP+∠ACN=90°,
∴CP⊥AC
∵OC是⊙O的半径
∴CP是⊙O的切线;
(2)∵∠ANC=90°,sin∠BCP=
,
∴
=
,
∴AC=5,
∴⊙O的半径为
如图,过点B作BD⊥AC于点D.
由(1)得BN=CN=
BC=
,
在Rt△CAN中,AN=
=2
在△CAN和△CBD中,
∠ANC=∠BDC=90°,∠ACN=∠BCD,
∴△CAN∽△CBD,
∴
=
,
∴BD=4.
在Rt△BCD中,CD=
=2,
∴AD=AC-CD=5-2=3,
∵BD∥CP,
∴
=
,
=
∴CP=
,BP=
∴△APC的周长是AC+PC+AP=20.
∵∠ABC=∠ACB,∴AB=AC,
∵AC是⊙O的直径,∴AN⊥BC,
∴∠CAN=∠BAN,BN=CN,
∵∠CAB=2∠BCP,
∴∠CAN=∠BCP.
∵∠CAN+∠ACN=90°,
∴∠BCP+∠ACN=90°,
∴CP⊥AC
∵OC是⊙O的半径
∴CP是⊙O的切线;
(2)∵∠ANC=90°,sin∠BCP=
| ||
| 5 |
∴
| CN |
| AC |
| ||
| 5 |
∴AC=5,
∴⊙O的半径为
| 5 |
| 2 |
如图,过点B作BD⊥AC于点D.
由(1)得BN=CN=
| 1 |
| 2 |
| 5 |
在Rt△CAN中,AN=
| AC2-CN2 |
| 5 |
在△CAN和△CBD中,
∠ANC=∠BDC=90°,∠ACN=∠BCD,
∴△CAN∽△CBD,
∴
| BC |
| AC |
| BD |
| AN |
∴BD=4.
在Rt△BCD中,CD=
| BC2-BD2 |
∴AD=AC-CD=5-2=3,
∵BD∥CP,
∴
| BD |
| CP |
| AD |
| AC |
| AD |
| DC |
| AB |
| BP |
∴CP=
| 20 |
| 3 |
| 10 |
| 3 |
∴△APC的周长是AC+PC+AP=20.


练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
 相交于点F、G.
相交于点F、G.


 点F,P为ED的延长线上一点.
点F,P为ED的延长线上一点.




