题目内容
已知关于 的方程
的方程 有两个不相等的实数根
有两个不相等的实数根 、
、 ,且
,且 .
.
(1)求证: ;
;
(2)试用 的代数式表示
的代数式表示 ;
;
(3)当 时,求
时,求 的值.
的值.
【答案】
(1)见解析(2) 或
或 (3)1
(3)1
【解析】⑴证明:∵关于 的方程
的方程 有两个不相等的实数根,
有两个不相等的实数根,
∴△= ,∴
,∴ .
.
又 ,∴
,∴ .
.
⑵ 或
或
(3)当 时,k=1.当
时,k=1.当 时,k不存在.所求的k的值为1
时,k不存在.所求的k的值为1
(1)方程有两个不相等的实数根,则△>0,建立关于n,k的不等式,结合不等式的性质,证出结论;
(2)根据根与系数的关系,把x1+x2=k代入已知条件(2x1+x2)2-8(2x1+x2)+15=0,即可用k的代数式表示x1;
(3)首先由(1)知n<-  k2,又n=-3,求出k的范围.再把(2)中求得的关系式代入原方程,即可求出k的值.
k2,又n=-3,求出k的范围.再把(2)中求得的关系式代入原方程,即可求出k的值.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
 的方程
的方程 的方程
的方程 有两个不相等的实数根,
有两个不相等的实数根, 的取值范围.②当k为最小整数时求原方程的解。
的取值范围.②当k为最小整数时求原方程的解。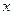 的方程
的方程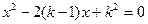 有两个实数根
有两个实数根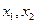 .
.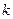 的取值范围;(4分)
的取值范围;(4分)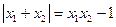 ,求
,求 的方程
的方程 有两个相等的实数根,那么m的值是 ▲ .
有两个相等的实数根,那么m的值是 ▲ . 的方程
的方程 有两个不相等的实数根
有两个不相等的实数根 、
、 ,且
,且 .
. ;
; 的代数式表示
的代数式表示 时,求
时,求