题目内容
如图，已知PA平分∠CAB，PC平分∠ACD，AB∥CD．求证：AP⊥PC．
证明：∵PA平分∠CAB，PC平分∠ACD，
∴∠PAC=
∠CAB，∠PCA=∠ACD
∴∠PAC+∠PCA=∠CAB+∠ACD=（∠CAB+∠ACD）
∵AB∥CD
∴∠CAB+∠ACD=180°
∴∠PAC+∠PCA=90°
∵△ACP中，∠PAC+∠PCA+∠P=180°
∴∠P=90°
∴AP⊥PC．
分析：先根据平行线的性质求出∠CAB+∠ACD的度数，再根据角平分线的性质求出∠PAC+∠PCA的度数，由三角形的内角和定理解答即可．
点评：考查平行线的性质及三角形内角和定理．两直线平行，同旁内角互补．角的等量代换的运用是正确解答本题的关键．
∴∠PAC=
∠CAB，∠PCA=∠ACD∴∠PAC+∠PCA=
∠CAB+∠ACD=（∠CAB+∠ACD）∵AB∥CD
∴∠CAB+∠ACD=180°
∴∠PAC+∠PCA=90°
∵△ACP中，∠PAC+∠PCA+∠P=180°
∴∠P=90°
∴AP⊥PC．
分析：先根据平行线的性质求出∠CAB+∠ACD的度数，再根据角平分线的性质求出∠PAC+∠PCA的度数，由三角形的内角和定理解答即可．
点评：考查平行线的性质及三角形内角和定理．两直线平行，同旁内角互补．角的等量代换的运用是正确解答本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
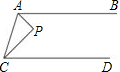如图，已知PA平分∠CAB，PC平分∠ACD，AB∥CD．求证：AP⊥PC．
如图，已知OP平分∠MON，PA⊥ON于点A，点Q是射线OM上的一个动点．若PA=2，则PQ的最小值为
如图，已知PA是∠MAN的平分线，B、C分别是AM、AN上的两点，若要△PAB≌△PAC，则需要添加的一个条件是