题目内容
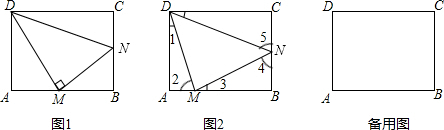
如图，D、E为△ABC两边AB、AC的中点，将△ABC沿线段DE折叠，使点A落在点F处，若∠B=55°，则∠BDF等于
- A.55°
- B.60°
- C.70°
- D.90°
C
分析：由于折叠，可得三角形全等，运用三角形全等得出∠ADE=∠FDE=55°，则∠BDF即可求．
解答：∵D、E为△ABC两边AB、AC的中点，即DE是三角形的中位线．
∴DE∥BC
∴∠ADE=∠B=55°
∴∠EDF=∠ADE=55°
∴∠BDF=180-55-55=70°．
故选C．
点评：本题考查了全等三角形的性质及三角形中位线的性质；解题的关键是，理解折叠就是得到全等的三角形，根据全等三角形的对应角相等就可以解决．
分析：由于折叠，可得三角形全等，运用三角形全等得出∠ADE=∠FDE=55°，则∠BDF即可求．
解答：∵D、E为△ABC两边AB、AC的中点，即DE是三角形的中位线．
∴DE∥BC
∴∠ADE=∠B=55°
∴∠EDF=∠ADE=55°
∴∠BDF=180-55-55=70°．
故选C．
点评：本题考查了全等三角形的性质及三角形中位线的性质；解题的关键是，理解折叠就是得到全等的三角形，根据全等三角形的对应角相等就可以解决．
练习册系列答案
相关题目
19、如图，D、E为AB、AC的中点，将△ABC沿线段DE折叠，使点A落在点F处，若∠B=50°，则∠BDF=
