题目内容
 如图,网格中的每个小正方形的边长都是1,A1、A2、A3、…都在格点上,△A1A2A3、△A3A4A5、△A5A6A7、…都是斜边在x轴上,且斜边长分别为2、4、6、…的等腰直角三角形.若△A1A2A3的三个顶点坐标为A1(2,0)、A2(1,-1)、A3(0,0),则依图中所示规律,A203的坐标为( )
如图,网格中的每个小正方形的边长都是1,A1、A2、A3、…都在格点上,△A1A2A3、△A3A4A5、△A5A6A7、…都是斜边在x轴上,且斜边长分别为2、4、6、…的等腰直角三角形.若△A1A2A3的三个顶点坐标为A1(2,0)、A2(1,-1)、A3(0,0),则依图中所示规律,A203的坐标为( )| A、(-100,0) |
| B、(100,0) |
| C、(-99,0) |
| D、(99,0) |
考点:规律型:点的坐标
专题:
分析:根据相邻的两个三角形有一个公共点列出与三角形的个数与顶点的个数的关系式,然后求出A203所在的三角形,并求出斜边长,然后根据第奇数个三角形关于直线x=1对称,第偶数个三角形关于直线x=2对称求出OA203,然后写出坐标即可.
解答:解:设到第n个三角形顶点的个数为y,
则y=2n+1,
∵当2n+1=203时,n=101,
∴A203是第101个三角形的最后一个顶点,
∵等腰直角三角形的斜边长分别为2、4、6、…,
∴第101个等腰直角三角形的斜边长为2×101=202,
由图可知,第奇数个三角形在x轴下方,关于直线x=1对称,
∴OA203=
-1=100,
∴A203的坐标为(-100,0).
故选A.
则y=2n+1,
∵当2n+1=203时,n=101,
∴A203是第101个三角形的最后一个顶点,
∵等腰直角三角形的斜边长分别为2、4、6、…,
∴第101个等腰直角三角形的斜边长为2×101=202,
由图可知,第奇数个三角形在x轴下方,关于直线x=1对称,
∴OA203=
| 202 |
| 2 |
∴A203的坐标为(-100,0).
故选A.
点评:本题是对点的坐标变化规律的考查,根据顶点个数与三角形的关系判断出A203所在的三角形是解题的关键.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
某学校生物兴趣小组11人到校外采集标本,其中3人每人采集4件,4人每人采集3件,4人每人采集5件,则这个兴趣小组平均每人采集标本是( )
| A、3件 | B、4件 | C、5件 | D、6件 |
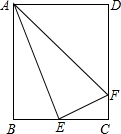 如图,矩形ABCD中,E是BC的中点,连接AE,过点E作EF⊥AE交DC于点F,连接AF.设
如图,矩形ABCD中,E是BC的中点,连接AE,过点E作EF⊥AE交DC于点F,连接AF.设| AB |
| AD |
(1)△ABE∽△ECF;(2)AE平分∠BAF;(3)当k=1时,△ABE∽△ADF;(4)tan∠EAF=k.
其中结论正确的是( )
| A、(1)(2)(3)(4) |
| B、(1)(3)(4) |
| C、(1)(2) |
| D、(2)(3) |
点P(2013,-2014)关于原点对称的点的坐标是( )
| A、(2013,2014) |
| B、(-2013,2014) |
| C、(-2013,-2014) |
| D、(-2013,-2014) |
 如图,在Rt△ABC中,∠C=90°,∠B=60°,内切圆O与边AB、BC、CA分别相切于点D、E、F,则∠DEF为( )
如图,在Rt△ABC中,∠C=90°,∠B=60°,内切圆O与边AB、BC、CA分别相切于点D、E、F,则∠DEF为( )| A、55° | B、60° |
| C、75° | D、80° |
 如图,在△ABC中,AB=AC,BD=CD,∠BAD=24°,AE=AD,则∠EDC的度数是
如图,在△ABC中,AB=AC,BD=CD,∠BAD=24°,AE=AD,则∠EDC的度数是 某海域有A、B、C三艘船正在捕鱼作业,C船突然出现故障,向A、B两船发出紧急求救信号,此时B船位于A船的北偏西72°方向,距A船24海里的海域,C船位于A船的北偏东33°方向,同时又位于B船的北偏东78°方向.
某海域有A、B、C三艘船正在捕鱼作业,C船突然出现故障,向A、B两船发出紧急求救信号,此时B船位于A船的北偏西72°方向,距A船24海里的海域,C船位于A船的北偏东33°方向,同时又位于B船的北偏东78°方向.