题目内容
 在?ABCD中,∠BAC=90°,AB=
在?ABCD中,∠BAC=90°,AB= ,BC=2AB,则AC=________,BD=________,?ABCD的面积是________.
,BC=2AB,则AC=________,BD=________,?ABCD的面积是________.

 2
2
分析:由∠BAC=90°,AB=
 ,BC=2AB,利用勾股定理即可求得AC的长,然后由平形四边形的性质,可求得OA的长,则可求得OB的长,继而求得答案.
,BC=2AB,利用勾股定理即可求得AC的长,然后由平形四边形的性质,可求得OA的长,则可求得OB的长,继而求得答案.解答:∵AB=
 ,BC=2AB,
,BC=2AB,∴BC=2
 ,
,∵∠BAC=90°,
∴在Rt△BAC中,AC=
 =
= ,
,∵四边形ABCD是平行四边形,
∴OA=
 AC=
AC= ,OB=
,OB= BD,
BD,∴在Rt△ABO中,OB=
 =
=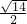 ,
,∴BD=2OB=
 ;
;∴S?ABCD=2S△ABC=2×
 AB•AC=
AB•AC= ×
× =2
=2 .
.故答案为:
 ,
, ,2
,2 .
.点评:此题考查了平行四边形的性质以及勾股定理.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
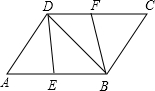 如图,在?ABCD中,E、F分别为边AB、CD的中点,连接DE、BF、BD.
如图,在?ABCD中,E、F分别为边AB、CD的中点,连接DE、BF、BD. 如图,在?ABCD中,EF∥AB,MN∥BC,MN与EF交于点O,且O点在对角线上,图中面积相等的四边形有( )
如图,在?ABCD中,EF∥AB,MN∥BC,MN与EF交于点O,且O点在对角线上,图中面积相等的四边形有( )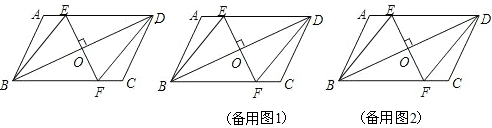
 如图,在?ABCD中,点E在边BC上,点F在BC的延长线上,且BE=CF.
如图,在?ABCD中,点E在边BC上,点F在BC的延长线上,且BE=CF.