Question

【题目】有两个函数y1和y2，若对于每个使函数有意义的实数x，函数y的值为两个函数值中较小的数，则称函数y为这两个函数y1、y2的较小值函数．例如：y1＝x+1，y2＝﹣2x+4，则y1，y2的较小值函数为y＝．

（1）函数y是函数y1＝，y2＝x的较小值函数．

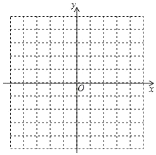
①在如图的平面直角坐标系中画出函数y的图象．

②写出函数y的两条性质．

（2）函数y是函数y1＝x2﹣2x+1，y2＝x+1的取较小值函数．a≤x≤时，函数值y的取值范围为0≤y≤b．当a取某个范围内的任意值时，b为定值．直接写出满足条件的a的取值范围及其对应的b的值．

（3）函数y是函数y1＝x2﹣2mx，y2＝mx（m为常数，且m≠0）的较小值函数．当m﹣2≤x≤1时，随着x的增大，函数y先增大后减小，直接写出m的取值范围．

Answer 1

【答案】(1)①见解析；②当x＜-1时，由y随x增大而增大；函数无最小值，有最大值1；
(2)；(3)或.

【解析】

（1）根据正比例函数和反比例函数图像描点画图，根据图像描述性质即可.

时，，当a取某个范围内的任意值时，b为定值，所以，；
由，得；当时对称轴；当时，；

解：如图1：

性质一：当x＜-1时，由y随x增大而增大，；
性质二：函数无最小值，有最大值1；





如图2：

时，且当a取某个范围内的任意值时，b为定值．
由图象可知，
；
，
，
，
，
当时，随着x的增大，函数y先增大后减小，故函数图像为y轴左侧一次函数图像，过原点和1之间取抛物线对称轴左侧图像.即对称轴在1的右侧，如图：

二次函数的对称轴，
；
当时，随着x的增大，函数y先增大后减小，故函数图像是抛物线对称轴右侧和y轴之间的一部分，过原点和1之间取一次函数.即抛物线对称轴在y左侧，如图：

，
；
综上所述：或；