题目内容
 (2011•辽阳)如图,等边△ABC的边长为4,M为BC上一动点(M不与B、C重合),若EB=1,∠EMF=60°,点E在AB边上,点F在AC边上.设BM=x,CF=y,则当点M从点B运动到点C时,y关于x的函数图象是( )
(2011•辽阳)如图,等边△ABC的边长为4,M为BC上一动点(M不与B、C重合),若EB=1,∠EMF=60°,点E在AB边上,点F在AC边上.设BM=x,CF=y,则当点M从点B运动到点C时,y关于x的函数图象是( )分析:利用等边三角形的性质和已知条件求得∠BEM=∠CMF,证得△BEM∽△CMF,利用相似三角形对应边成比例得到两变量之间的函数关系式即可确定其图象.
解答:解:∵△ABC为等边三角形,
∴∠B=∠C=60°,
∴∠BEM+∠BME=∠FMC+∠MFC=120°,
∵∠EMF=60°,
∴∠EMB+∠FMC=120°,
∴∠BEM=∠CMF,
∴△BEM∽△CMF,
∴
=
设BM=x,CF=y,
∴CM=4-x,
∴
=
,
整理得:y=-x2+4x=-(x-2)2+4,
故选B.
∴∠B=∠C=60°,
∴∠BEM+∠BME=∠FMC+∠MFC=120°,
∵∠EMF=60°,
∴∠EMB+∠FMC=120°,
∴∠BEM=∠CMF,
∴△BEM∽△CMF,
∴
| BE |
| CM |
| BM |
| CF |
设BM=x,CF=y,
∴CM=4-x,
∴
| 1 |
| 4-x |
| x |
| y |
整理得:y=-x2+4x=-(x-2)2+4,
故选B.
点评:考查了动点问题的函数图象,此题为动点函数问题,关键列出动点的函数关系,再判断选项.

练习册系列答案
相关题目
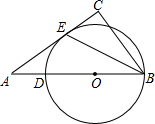 (2011•辽阳)如图,⊙O经过点B、D、E,BD是⊙O的直径,∠C=90°,BE平分∠ABC.
(2011•辽阳)如图,⊙O经过点B、D、E,BD是⊙O的直径,∠C=90°,BE平分∠ABC.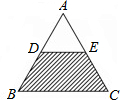 (2011•辽阳)如图,已知等边△ABC的面积为1,D、E分别为AB、AC的中点,若向图中随机抛掷一枚飞镖,飞镖落在阴影区域的概率是(不考虑落在线上的情形)( )
(2011•辽阳)如图,已知等边△ABC的面积为1,D、E分别为AB、AC的中点,若向图中随机抛掷一枚飞镖,飞镖落在阴影区域的概率是(不考虑落在线上的情形)( ) (2011•辽阳)如图,AB为⊙O直径,CD⊥AB,∠BDC=35°,则∠CAD=
(2011•辽阳)如图,AB为⊙O直径,CD⊥AB,∠BDC=35°,则∠CAD= (2011•辽阳)如图,已知菱形ABCD的边长为2,∠BAD=60°,若DE⊥AB,垂足为点E,则DE的长为
(2011•辽阳)如图,已知菱形ABCD的边长为2,∠BAD=60°,若DE⊥AB,垂足为点E,则DE的长为 梯形?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
梯形?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.