题目内容
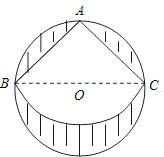 如图:有一个直径为
如图:有一个直径为| 2 |
(1)求被剪掉的阴影部分的面积.
(2)用所留的扇形纸片围成一个圆锥,则圆锥的底面圆的半径是多少?
(3)求圆锥的全面积.
分析:(1)被剪掉的阴影部分的面积=圆的面积-扇形的面积;
(2)圆锥的底面圆的半径=扇形的弧长÷2π;
(3)圆锥的全面积=圆锥的侧面积+圆锥的底面积.
(2)圆锥的底面圆的半径=扇形的弧长÷2π;
(3)圆锥的全面积=圆锥的侧面积+圆锥的底面积.
解答:解:(1)∵∠A=90°,
∴BC为直径,AB=AC,
∴AB=AC=1,
∴被剪掉的阴影部分的面积为:π×(
)2-
=
平方米;
(2)圆锥的底面圆的半径=
÷2π=
米;
(3)圆锥的全面积=
+π(
)2=
π平方米.
∴BC为直径,AB=AC,
∴AB=AC=1,
∴被剪掉的阴影部分的面积为:π×(
| ||
| 2 |
| 90π×12 |
| 360 |
| π |
| 4 |
(2)圆锥的底面圆的半径=
| 90π×1 |
| 180 |
| 1 |
| 4 |
(3)圆锥的全面积=
| 90π×12 |
| 360 |
| 1 |
| 4 |
| 5 |
| 16 |
点评:本题考查圆锥的各方面的计算,注意利用圆锥的底面周长等于扇形的弧长这个等量关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
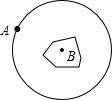 如图,有一个直径为100m的圆形湖泊,岸边有一个小木柱A,湖中央有一小岛,在小岛的中心打下小木柱B.一个人不会游泳,但他有一条绳子,这条绳子比100m长一些,用什么方式他能利用绳子和小木柱横渡到小岛上?
如图,有一个直径为100m的圆形湖泊,岸边有一个小木柱A,湖中央有一小岛,在小岛的中心打下小木柱B.一个人不会游泳,但他有一条绳子,这条绳子比100m长一些,用什么方式他能利用绳子和小木柱横渡到小岛上? 米的圆形纸片,要从中剪出一个最大的圆心角是90°的扇形ABC.
米的圆形纸片,要从中剪出一个最大的圆心角是90°的扇形ABC.
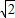 米的圆形纸片,要从中剪出一个最大的圆心角是90°的扇形ABC.
米的圆形纸片,要从中剪出一个最大的圆心角是90°的扇形ABC.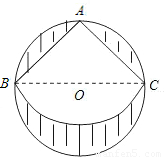
 米的圆形纸片,要从中剪出一个最大的圆心角是90°的扇形ABC.
米的圆形纸片,要从中剪出一个最大的圆心角是90°的扇形ABC.