题目内容
已知抛物线y=ax2+( +3a)x+4与x轴交于A、B两点,与y轴交于点C.是否存在实数a,使得△ABC为直角三角形?若存在,请求出a的值;若不存在,请说明理由.
+3a)x+4与x轴交于A、B两点,与y轴交于点C.是否存在实数a,使得△ABC为直角三角形?若存在,请求出a的值;若不存在,请说明理由.
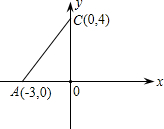 解:依题意,得点C的坐标为(0,4),
解:依题意,得点C的坐标为(0,4),设点A、B的坐标分别为(x1,0),(x2,0),
由ax2+(
 +3a)x+4=0,
+3a)x+4=0,解得x1=-3,x2=-
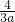 ,
,∴点A、B的坐标分别为(-3,0),(
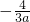 ,0),
,0),∴AB=|-
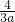 +3|,AC=
+3|,AC=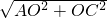 =5,BC=
=5,BC=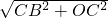 =
=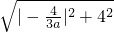 ,
,∴AB2=|-
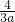 +3|2=
+3|2=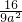 -
-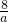 +9,
+9,AC2=25,BC2=
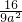 +16.
+16.(ⅰ)当AB2=AC2+BC2时,∠ACB=90°,
由AB2=AC2+BC2,
得
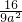 -
-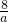 +9=25+
+9=25+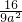 +16,
+16,解得a=-
 ,
,∴当a=-
 时,点B的坐标为(
时,点B的坐标为( ,0),
,0),AB2=
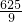 ,AC2=25,BC2=
,AC2=25,BC2=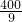 ,
,于是AB2=AC2+BC2,
∴当a=-
 时,△ABC为直角三角形.
时,△ABC为直角三角形.(ⅱ)当AC2=AB2+BC2时,∠ABC=90°,
由AC2=AB2+BC2,
得25=
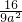 -
-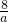 +9+
+9+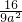 +16,
+16,解得a=
 .
.当a=
 时,-
时,-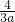 =-
=- =-3,点B(-3,0)与点A重合,不合题意.
=-3,点B(-3,0)与点A重合,不合题意.<ⅲ>当BC2=AC2+AB2时,∠BAC=90°,
由BC2=AC2+AB2,
得25+
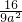 -
-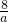 +9=
+9=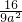 +16,
+16,解得a=
 ,
,不合题意.
综合<ⅰ>、<ⅱ>、<ⅲ>,当a=-
 时,△ABC为直角三角形.
时,△ABC为直角三角形.分析:可根据抛物线的解析式表示出A、B、C的坐标,然后分别表示出AB、AC、BC的长,可根据∠BAC=90°,∠BCA=90°,∠ABC=90°三种不同情况用勾股定理求出a的值.
点评:本题考查了二次函数的应用、直角三角形的判定和勾股定理等知识.

练习册系列答案
相关题目
 与x轴的另一个交点为E.
与x轴的另一个交点为E. 如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=
如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=