题目内容
如图1,一副直角三角板满足AB=BC,AC=DE,∠ABC=∠DEF=90°∠EDF=30°,【操作1】将三角板DEF的直角顶点E放置于三角板ABC的斜边AC上,再将三角板DEF绕点E旋转,并使边DE与边AB交于点P,边EF与边BC于点Q.
在旋转过程中,如图2,当
 时,EP与EQ满足怎样的数量关系?并给出证明.
时,EP与EQ满足怎样的数量关系?并给出证明.【操作2】在旋转过程中,如图3,当
 时EP与EQ满足怎样的数量关系?,并说明理由.
时EP与EQ满足怎样的数量关系?,并说明理由.【总结操作】根据你以上的探究结果,试写出
 当时,EP与EQ满足的数量关系是什么?其中m的取值范围是什么?(直接写出结论,不必证明)m.
当时,EP与EQ满足的数量关系是什么?其中m的取值范围是什么?(直接写出结论,不必证明)m.
【答案】分析:(操作1)连接BE,根据已知条件得到E是AC的中点,根据等腰直角三角形的性质可以证明DE=CE,∠PBE=∠C.根据等角的余角相等可以证明∠BEP=∠CEQ.即可得到全等三角形,从而证明结论;
(操作2)作EM⊥AB,EN⊥BC于M、N,根据两个角对应相等证明△MEP∽△NWQ,发现EP:EQ=EM:EN,再根据等腰直角三角形的性质得到EM:EN=AE:CE;
(总结操作)根据(2)中求解的过程,可以直接写出结果;要求m的取值范围,根据交点的位置的限制进行分析.
解答: (操作1)EP=EQ,
(操作1)EP=EQ,
证明:连接BE,根据E是AC的中点和等腰直角三角形的性质,得:BE=CE,∠PBE=∠C=45°,
∵∠BEC=∠FED=90°
∴∠BEP=∠CEQ,
在△BEP和△CEQ中
 ,
,
∴△BEP≌△CEQ(ASA),
∴EP=EQ;
如图2,EP:EQ=EM:EN=AE:CE=1:2,
理由是:作EM⊥AB,EN⊥BC于M,N,
∴∠EMP=∠ENC,
∵∠MEP+∠PEN=∠PEN+∠NEF=90°,
∴∠MEP=∠NEF,
∴△MEP∽△NEQ,
∴EP:EQ=EM:EN=AE:CE=1:2;
如图3,过E点作EM⊥AB于点M,作EN⊥BC于点N,
∵在四边形PEQB中,∠B=∠PEQ=90°,
∴∠EPB+∠EQB=180°,
又∵∠EPB+∠MPE=180°,
∴∠MPE=∠EQN,
∴Rt△MEP∽Rt△NEQ,
∴ =
= ,
,
Rt△AME∽Rt△ENC,
∴ =m=
=m= ,
,
∴ =1:m=
=1:m= ,
,
EP与EQ满足的数量关系式1:m,即EQ=mEP,
∴0<m≤2+ ,(因为当m>2+
,(因为当m>2+ 时,EF和变成不相交);
时,EF和变成不相交);
点评:本题考查了相似三角形的性质和判定,全等三角形的性质和判定,主要考查学生运用定理进行推理的能力,证明过程类似.
(操作2)作EM⊥AB,EN⊥BC于M、N,根据两个角对应相等证明△MEP∽△NWQ,发现EP:EQ=EM:EN,再根据等腰直角三角形的性质得到EM:EN=AE:CE;
(总结操作)根据(2)中求解的过程,可以直接写出结果;要求m的取值范围,根据交点的位置的限制进行分析.
解答:
 (操作1)EP=EQ,
(操作1)EP=EQ,证明:连接BE,根据E是AC的中点和等腰直角三角形的性质,得:BE=CE,∠PBE=∠C=45°,
∵∠BEC=∠FED=90°
∴∠BEP=∠CEQ,
在△BEP和△CEQ中
 ,
,∴△BEP≌△CEQ(ASA),
∴EP=EQ;
如图2,EP:EQ=EM:EN=AE:CE=1:2,
理由是:作EM⊥AB,EN⊥BC于M,N,
∴∠EMP=∠ENC,
∵∠MEP+∠PEN=∠PEN+∠NEF=90°,
∴∠MEP=∠NEF,
∴△MEP∽△NEQ,
∴EP:EQ=EM:EN=AE:CE=1:2;
如图3,过E点作EM⊥AB于点M,作EN⊥BC于点N,
∵在四边形PEQB中,∠B=∠PEQ=90°,
∴∠EPB+∠EQB=180°,
又∵∠EPB+∠MPE=180°,
∴∠MPE=∠EQN,
∴Rt△MEP∽Rt△NEQ,
∴
 =
= ,
,Rt△AME∽Rt△ENC,
∴
 =m=
=m= ,
,∴
 =1:m=
=1:m= ,
,EP与EQ满足的数量关系式1:m,即EQ=mEP,
∴0<m≤2+
 ,(因为当m>2+
,(因为当m>2+ 时,EF和变成不相交);
时,EF和变成不相交);点评:本题考查了相似三角形的性质和判定,全等三角形的性质和判定,主要考查学生运用定理进行推理的能力,证明过程类似.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
 26、如图,一副三角饭的两个直角顶点重合在一起,
26、如图,一副三角饭的两个直角顶点重合在一起,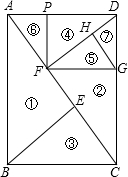 知线段AB=1,∠BAC=θ.
知线段AB=1,∠BAC=θ.

