Question

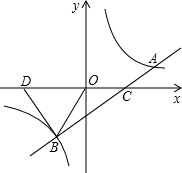
如图，已知反比例函数y=

k1

2x

的图象与一次函数y=k₂x+b的图象交于A，B两点，A（1，n），B（-

1

2

，-2）．
（1）求反比例函数和一次函数的解析式；
（2）在x轴上是否存在点P，使△AOP为等腰三角形？若存在，请你直接写出P点的坐标；若不存在，请说明理由．

Answer 1

（1）∵点B（-

1

2

，-2）在反比例函数y=

k1

2x

图象上，
∴-2=

k1

2×(- 1 2 )

∴k₁=2
∴反比例函数的解析式为y=

1

x

，（2分）
又∵A（1，n）在反比例函数图象上，
∴n=

1

1

，
∴n=1；
∴A点坐标为（1，1）；
∴一次函数y=k₂x+b的图象经过点A（1，1），B（-

1

2

，-2）；
∴

k2+b=1 - 1 2 k2+b=-2

，∴

k2=2 b=-1

；
∴一次函数的解析式为y=2x-1；（4分）

（2）存在符合条件的点P．（5分）
若OA=OP，则P（

2

，0）或（-

2

，0），
若AP=OA，则P（2，0），
若OP=AP，则（1，0），
可求出点P的坐标为（

2

，0），（-

2

，0），（2，0），（1，0）．（7分）