Question

1．在等腰Rt△ABC中，AB=BC，DC⊥BC，在AC上取一点E，使BE⊥DE，求证BE=DE．

Answer 1

分析 如图，作EM⊥BC于M，EN⊥CD于N，只要证明△EMB≌△END即可．

解答 证明：如图，作EM⊥BC于M，EN⊥CD于N．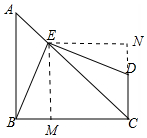

∵BA=BC，∠ABC=90°，
∴∠ACB=45°，
∵DC⊥BC，
∴∠DCB=90°，
∴∠DCA=∠BCA=45°，
∵EM⊥BC于M，EN⊥CD于N，
∴EM=EN，
∵∠EMC=∠N=∠MCN=90°，
∴∠MEN=90°，
∵BE⊥ED，
∴∠BED=∠MEN，
∴∠BEM=∠DEN，
在△EMB和△END中，
$\left\{\begin{array}{l}{∠BEM=∠DEN}\\{EM=EN}\\{∠EMB=∠N=90°}\end{array}\right.$，
∴△EMB≌△END，
∴BE=ED．

点评 本题考查全等三角形的判定和性质、等腰直角三角形的性质．角平分线的性质定理等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考常考题型．