题目内容
函数
的图象的两个分支分别在第二、四象限内，则k的取值范围是________．
k＜1
分析：根据反比函数图象的性质，当反比例系数k-1＜0时，图象在第二、四象限，即可求出k的取值范围．
解答：∵，其图象的两个分支分别位于第二、四象限，
∴k-1＜0，
解得：k＜1，
故答案为：k＜1．
点评：本题考查了反比例函数的图象和性质，属于基础题，主要掌握①、当k＞0时，图象分别位于第一、三象限；当k＜0时，图象分别位于第二、四象限．②、当k＞0时，在同一个象限内，y随x的增大而减小；当k＜0时，在同一个象限，y随x的增大而增大．
分析：根据反比函数图象的性质，当反比例系数k-1＜0时，图象在第二、四象限，即可求出k的取值范围．
解答：∵
，其图象的两个分支分别位于第二、四象限，∴k-1＜0，
解得：k＜1，
故答案为：k＜1．
点评：本题考查了反比例函数的图象和性质，属于基础题，主要掌握①、当k＞0时，图象分别位于第一、三象限；当k＜0时，图象分别位于第二、四象限．②、当k＞0时，在同一个象限内，y随x的增大而减小；当k＜0时，在同一个象限，y随x的增大而增大．
练习册系列答案
黄冈小状元同步计算天天练系列答案
相关题目
如图，在平面直角坐标系xOy中，已知矩形AOBC，AO=2，BO=3，函数
的图象经过点C．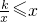
时x的取值范围．
的图象的两个分支分别别位于第二、四象限，则m的取值范围是____________________.
的图象的两个分支关于
_______ 对称.
的图象的两个分支分别别位于第二、四象限，则m的取值范围是____________________.
的图象的两个分支分别别位于第二、四象限，则m的取值范围是______________.