题目内容
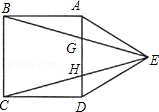
如图,在正方形ABCD中,E是BC上的一点,连接AE,作BF⊥AE,垂足为H,交CD于F,作CG∥AE,交BF于G.求证:
(1)CG=BH;
(2)FC2=BF•GF;
(3) =
=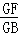 .
.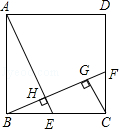
(1)CG=BH;
(2)FC2=BF•GF;
(3)
 =
=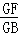 .
.
(1)△ABH≌△BCG,∴CG=BH (2)△CFG∽△BFC,∴ =
= ,即FC2=BF•GF
,即FC2=BF•GF
(3)∵AB=BC,∴AB2=BG•BF(具体过程见解析)
 =
= ,即FC2=BF•GF
,即FC2=BF•GF(3)∵AB=BC,∴AB2=BG•BF(具体过程见解析)
试题分析:(1)∵BF⊥AE,CG∥AE,
∴CG⊥BF,
∵在正方形ABCD中,∠ABH+∠CBG=90°,∠CBG+∠BCG=90°,
∠BAH+∠ABH=90°,
∴∠BAH=∠CBG,∠ABH=∠BCG,
AB=BC,
∴△ABH≌△BCG,
∴CG=BH;
(2)∵∠BFC=∠CFG,∠BCF=∠CGF=90°,
∴△CFG∽△BFC,
∴
 =
= ,
,即FC2=BF•GF;
(3)由(2)可知,BC2=BG•BF,
∵AB=BC,
∴AB2=BG•BF,
∴
 =
= =
= ,
,即
 =
= .
.
点评:本题考查了相似三角形的判定与性质,全等三角形的判定与性质,正方形的性质.关键是由垂足得出互余关系求角相等,由边相等证明三角形全等,由角相等证明相似三角形,利用性质解题.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目

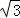 S2
S2