题目内容
(本题满分12分)如图,在数轴上点A、B、C表示的数分别为-2,1,6,点A与点B之间的距离表示为AB,点B与点C之间的距离表示为BC,点A与点C之间的距离表示为AC.

(1)则AB= ,BC= ,AC= ;
(2)点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动。请问:BC-AB的值是否随着运动时间t的变化而改变?若变化,请说明理由;若不变,请求其值;
(3)由第(1)小题可以发现,AB+BC=AC.若点C以每秒3个单位长度的速度向左运动,同时,点A和点B分别以每秒1个单位长度和每秒2个单位长度的速度向右运动.请问:随着运动时间t的变化, AB、BC、AC之间是否存在类似于(1)的数量关系?请说明理由.
(1)AB= 3 ,BC= 5 ,AC= 8 .
(2)BC-AB的值不会随着时间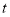 的变化而改变.
的变化而改变.
BC-AB=(5t-2t+5)-(t+2t+3)=2 ;
(3)存在,
AB=t+3
BC=5-5t(t≤1时) 或 BC=5t-5 (t>1时)
AC=8-4t (t≤2时) 或 AC=4t-8(t>2)
当t≤1时,AB+BC=(t+3)+(5-5t)=8-4t=AC
当1<t≤2时,BC+AC=(5t-5)+(8-4t)=t+3=AB
当t>2时,AB+AC=(t+3)+(4t-8)=5t-5=BC.
【解析】
试题分析:(1)根据数轴上两点间的距离直接可得线段长度;
要想知道(BC-AB)是否随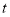 的变化而变化,就要看表示(BC-AB)的代数式是否与t有关,是否含有t.可用含t的代数式把(BC-AB)表示出来再化简,再作判断;
的变化而变化,就要看表示(BC-AB)的代数式是否与t有关,是否含有t.可用含t的代数式把(BC-AB)表示出来再化简,再作判断;
(3)借助数轴先用t表示AB、BC、AC的长度,AB=t+3;BC=5-5t(t≤1) 或 BC=5t-5 (t>1);AC=8-4t (t≤2时) 或 AC=4t-8(t>2).再根据t的取值来分情况讨论.
试题解析:(1)AB= 3 ,BC= 5 ,AC= 8 .
(2)因为A、B两点是反向运动,所以AB=t+2t+3;因为B、C两点是同向运动,所以BC=(5t-2t+5).可得BC-AB=(5t-2t+5)-(t+2t+3)=2,即无论t取何值,BC-AB都是2,不会变化;
(3)根据题意可知:
AB=2t+3-t=t+3;
BC=5-2t-3t= 5-5t(t≤1时) 或 BC=2t+3t-5=5t-5 (t>1时);
AC=8-t-3t=8-4t (t≤2时) 或 AC=t+3t-8=4t-8(t>2).
当t≤1时,AB+BC=(t+3)+(5-5t)=8-4t=AC;
当1<t≤2时,BC+AC=(5t-5)+(8-4t)=t+3=AB;
当t>2时,AB+AC=(t+3)+(4t-8)=5t-5=BC.
所以,随着运动时间t的变化, AB、BC、AC之间存在类似于(1)的数量关系.
考点:(1)数轴上两点间的距离;(2)用代数式表示数量关系;(3)整式的加减.
考点分析: 考点1:有理数 1、有理数的概念:正数和分数统称为有理数.2、有理数的分类:
①按整数、分数的关系分类; ②按正数、负数与0的关系分类.
有理数{整数{正整数0负整数分数{正分数负分数 有理数 {正数{正整数正分数0负数{负整数负分数
注意:如果一个数是小数,它是否属于有理数,就看它是否能化成分数的形式,所有的有限小数和无限循环小数都可以化成分数的形式,因而属于有理数,而无限不循环小数,不能化成分数形式,因而不属于有理数. 试题属性
- 题型:
- 难度:
- 考核:
- 年级:

 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ,其中m是方程
,其中m是方程 的根.
的根.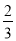 、9、
、9、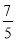 、-(-8)、0、-|+3|,负有理数有( )
、-(-8)、0、-|+3|,负有理数有( )
 -︱-5︱____ -(-1)
-︱-5︱____ -(-1)



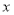 元,可得方程 .
元,可得方程 .
 的顶点坐标是( )
的顶点坐标是( )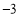 ) B、(
) B、(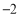 ,3) C、(2,3) D、(
,3) C、(2,3) D、(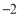 ,
,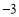 )
)