题目内容
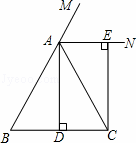
已知△ABC中,M为BC的中点,直线m绕点A旋转,过B、M、C分别作BD⊥m于D,ME⊥m于E,CF⊥m于F.
(1)当直线m经过B点时,如图1,易证EM=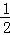 CF.(不需证明)
CF.(不需证明)
(2)当直线m不经过B点,旋转到如图2、图3的位置时,线段BD、ME、CF之间有怎样的数量关系?请直接写出你的猜想,并选择一种情况加以证明.
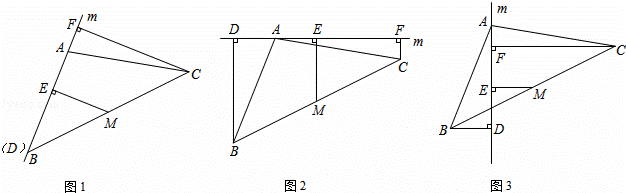
解:(1)如图1,
∵ME⊥m于E,CF⊥m于F,
∴ME∥CF,
∵M为BC的中点,
∴E为BF中点,
∴ME是△BFC的中位线,
∴EM= CF.
CF.
(2)图2的结论为:ME= (BD+CF),
(BD+CF),
图3的结论为:ME= (CF﹣BD).
(CF﹣BD).
图2的结论证明如下:连接DM并延长交FC的延长线于K
又∵BD⊥m,CF⊥m
∴BD∥CF
∴∠DBM=∠KCM
在△DBM和△KCM中
 ,
,
∴△DBM≌△KCM(ASA),
∴DB=CK DM=MK
由题意知:EM= FK,
FK,
∴ME= (CF+CK)=
(CF+CK)= (CF+DB)
(CF+DB)
图3的结论证明如下:连接DM并延长交FC于K
又∵BD⊥m,CF⊥m
∴BD∥CF
∴∠MBD=∠KCM
在△DBM和△KCM中
 ,
,
∴△DBM≌△KCM(ASA)
∴DB=CK,DM=MK,
由题意知:EM= FK,
FK,
∴ME= (CF﹣CK)=
(CF﹣CK)= (CF﹣DB).
(CF﹣DB).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案如图(十三),矩形ABCD的外接圆O与水平地面相切于A点,圆O半径为2,且 =2
=2 。若在没有滑动的情况下,将圆O向右滚动,使得O点向右移动了75p,则此时哪一弧与地面相切?
。若在没有滑动的情况下,将圆O向右滚动,使得O点向右移动了75p,则此时哪一弧与地面相切?
(A) 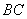 (B)
(B) 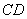 (C)
(C)  (D)
(D) 
 |
如图,在平面直角坐标系中,反比例函数y1= 的图象与一次函数y2=kx=b的图象交于A、B两点.若y1<y2,则x的取值范围是( )
的图象与一次函数y2=kx=b的图象交于A、B两点.若y1<y2,则x的取值范围是( )

|
| A. | 1<x<3 | B. | x<0或1<x<3 | C. | 0<x<1 | D. | x>3或0<x<1 |

 ﹣
﹣ ÷
÷ ,其中x=4cos60°+1.
,其中x=4cos60°+1. )3 +(-
)3 +(- )4 之值为何?
)4 之值为何? (B) -16+16
(B) -16+16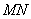 ,再将纸片展开后,M、N 两点分别在
,再将纸片展开后,M、N 两点分别在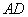 、
、