Question

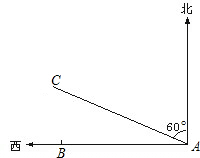
如图，从A地到B地的公路需要经过C地，图中AC=10千米，∠CAB=25°，∠CBA=37°。因城市规划的需要，将在A，B两地之间修建一条笔直的公路。
（1）求改直后的公路AB的长；
（2）问：公路改造后比原来缩短了多少千米？
（sin25°≈0.42，cos25°≈0.91，sin37°≈0.60，tan37°≈0.75）

Answer 1

（1）AB= 14.7（千米）（2）改直后的路程缩短了2.3千米

试题分析：（1）作CH⊥AB于点H，利用三角函数即可得
（2）利用三角函数求得BC，然后AC+BC-AB就可以了
试题解析：解：（1）作CH⊥AB于点H，在Rt△ACH中，

CH=ACsin∠CAB=ACsin25°=10×0.42=4.2
AH=ACcos∠CAB=ACcos25°=10×0.91=9.1
在Rt△B CH中，
BH=CH÷tan37°=42÷0.75=5.6
∴AB=AH+BH=9.1+5.6=14.7（千米）
（2）BC=CH÷sin37°=4.2÷0.60=7.0
∴AC+BC-AB=10+7-14.7=2.3（千米）
答：改直后的路程缩短了2.3千米。