题目内容
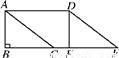
如图,在△ABC中,∠B=90°,AB=6 cm,BC=8 cm.将△ABC沿射线BC方向平移10 cm,得到△DEF,A,B,C的对应点分别是D,E,F,连接AD.
求证:四边形ACFD是菱形.
练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
题目内容
如图,在△ABC中,∠B=90°,AB=6 cm,BC=8 cm.将△ABC沿射线BC方向平移10 cm,得到△DEF,A,B,C的对应点分别是D,E,F,连接AD.
求证:四边形ACFD是菱形.

 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案