题目内容

抛物线y=x²-4x+5的最小值为________．

1
分析：本题由于二次项的系数为1，可用配方法求解．
解答：y=x²-4x+5=（x-2）²+1，由于函数开口向上，因此函数有最小值，且最小值为1．
点评：求二次函数的最大（小）值有三种方法，第一种可由图象直接得出，第二种是配方法，第三种是公式法．

练习册系列答案

智能测评与辅导系列答案

小考加速度系列答案

百校名师阅读真题80篇系列答案

新阅读与作文系列答案

中考全程总复习系列答案

阅读课堂北京教育出版社系列答案

1日1练口算题卡系列答案

举一反三同步巧讲精练系列答案

口算与应用题卡系列答案

培优新题库系列答案

相关题目

现有A、B两枚均匀的小立方体（立方体的每个面上分别标有数字1、2、3、4、5、6），小明用掷A立方体朝上的数字为x，掷B立方体朝上的数字为y来确定点P（x，y），则小明各掷一次确定的点P落在已知抛物线y=-x²+4x+3上的概率是

5、抛物线y=x²-4x+2的顶点坐标是（　　）

A、（-2，-2）

B、（2，-2）

C、（2，2）

D、（-2，2）

9、抛物线y=x²+4x-1的对称轴、顶点坐标分别为（　　）

A、直线x=4、（4，-1）

B、直线x=2、（2，-1）

C、直线x=2、（4，-5）

D、直线x=-2、（-2，-5）

抛物线y=x²+4x+3在x轴上截得的线段的长度是

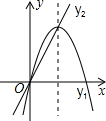如图，抛物线y1=-x2+4x和直线y₂=2x．当y₁＞y₂时，x的取值范围是（　　）

B、x＜0或x＞2

C、x＜0或x＞4