Question

如图①，正方形ABCD的顶点A,B的坐标分别为，顶点C,D在第一象限．点P从点A出发，沿正方形按逆时针方向匀速运动，同时，点Q从点E(4,0)出发，沿x轴正方向以相同速度运动．当点P到达点C时，P,Q两点同时停止运动，设运动的时间为t秒．

（1）求正方形ABCD的边长．

（2）当点P在AB边上运动时，△OPQ的面积S（平方单位）与时间t（秒）之间的函数图象为抛物线的一部分（如图②所示），求P,Q两点的运动速度．

（3）求（2）中面积S（平方单位）与时间t（秒）的函数关系式及面积取最大值时点的坐标．

（4）若点P,Q保持（2）中的速度不变，则点P沿着AB边运动时，∠OPQ的大小随着时间的增大而增大；沿着BC边运动时，∠OPQ的大小随着时间的增大而减小．当点沿着这两边运动时，使∠OPQ=90°的点有　　　　　个．

Answer 1

解：（1）作BF⊥y轴于F。

因为A（0，10），B（8，4）

所以FB=8，FA=6

所以

（2）由图2可知，点P从点A运动到点B用了10秒。

又因为AB=10，10÷10=1

所以P、Q两点运动的速度均为每秒1个单位。

（3）方法一：作PG⊥y轴于G

则PG//BF

所以，即

所以

所以

因为OQ=4+t

所以

即

因为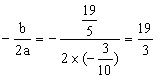

且

当时，S有最大值。

方法二：当t=5时，OG=7，OQ=9

设所求函数关系式为

因为抛物线过点（10，28），（5，）

所以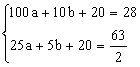

所以

所以

因为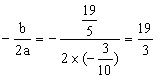

且

当时，S有最大值。

此时

所以点P的坐标为（）。

（4）当点P沿AB边运动时，∠OPQ由锐角→直角→钝角；当点P沿BC边运动时，∠OPQ由钝角→直角→锐角（证明略），故符合条件的点P有2个。