题目内容
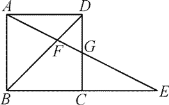
【题目】如图,已知![]() ,
,![]() 和
和![]() 分别平分
分别平分![]() 和
和![]() ,
,![]() ,则
,则![]() 的度数为( )
的度数为( )

A. 16°B. 32°C. 48°D. 64°
【答案】B
【解析】
已知BE和DF分别平分∠ABF和∠CDE,根据角平分线分定义可得∠ABE=![]() ∠ABF,∠CDF=
∠ABF,∠CDF=![]() ∠CDE;过点E作EM
∠CDE;过点E作EM![]() AB,点F作FN
AB,点F作FN![]() AB,即可得
AB,即可得![]() EM
EM![]() FN,由平行线的性质可得∠ABE=∠BEM,∠MED=∠EDC,∠ABF=∠BFN,∠CDF=∠DFN,由此可得∠BED=∠BEM+∠DEM=∠ABE+∠CDE=
FN,由平行线的性质可得∠ABE=∠BEM,∠MED=∠EDC,∠ABF=∠BFN,∠CDF=∠DFN,由此可得∠BED=∠BEM+∠DEM=∠ABE+∠CDE=![]() ∠ABF+∠CDE,∠BFD=∠BFN+∠DFN=∠ABF+∠CDF=∠ABF +
∠ABF+∠CDE,∠BFD=∠BFN+∠DFN=∠ABF+∠CDF=∠ABF +![]() ∠CDE, 又因2∠BED-∠BFD=48°,即可得2(
∠CDE, 又因2∠BED-∠BFD=48°,即可得2(![]() ∠ABF+∠CDE)-(∠ABF +
∠ABF+∠CDE)-(∠ABF +![]() ∠CDE)=48°,由此即可求得∠CDE=32°.
∠CDE)=48°,由此即可求得∠CDE=32°.
∵BE和DF分别平分∠ABF和∠CDE,
∴∠ABE=![]() ∠ABF,∠CDF=
∠ABF,∠CDF=![]() ∠CDE,
∠CDE,
过点E作EM![]() AB,点F作FN
AB,点F作FN![]() AB,
AB,

∵![]() ,
,
∴![]() EM
EM![]() FN,
FN,
∴∠ABE=∠BEM,∠MED=∠EDC,∠ABF=∠BFN,∠CDF=∠DFN,
∴∠BED=∠BEM+∠DEM=∠ABE+∠CDE=![]() ∠ABF+∠CDE,
∠ABF+∠CDE,
∠BFD=∠BFN+∠DFN=∠ABF+∠CDF=∠ABF +![]() ∠CDE,
∠CDE,
∵2∠BED-∠BFD=48°,
∴2(![]() ∠ABF+∠CDE)-(∠ABF +
∠ABF+∠CDE)-(∠ABF +![]() ∠CDE)=48°,
∠CDE)=48°,
∴∠CDE=32°.
故选B.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目