题目内容
 如图,小正方形的边长均为1,每个小格的顶点称为格点,以格点连线为边的三角形叫格点三角形.在如图5×5的方格中,作格点三角形和△ABC相似,则所作的格点三角形中,最小面积和最大面积分别为( )
如图,小正方形的边长均为1,每个小格的顶点称为格点,以格点连线为边的三角形叫格点三角形.在如图5×5的方格中,作格点三角形和△ABC相似,则所作的格点三角形中,最小面积和最大面积分别为( )| A、0.5,2.5 | B、0.5,5 | C、1,2.5 | D、1,5 |
分析:作出面积最小和面积最大的格点三角形,因为相似三角形的面积比等于相似比的平方,所以此题只要求得两三角形的一组对应边的比即可.根据格点三角形边长的求解方法,易得AB,DE与GH的长.即可得出问题的解.
解答:解:如图所示,△DEF和△GHI分别是面积最小和面积最大的三角形.

因为△DEF,△GHI和△ABC都相似,AB=
,DE=1,GH=
,
所以它们的相似比为DE:AB=1:
,GH:AB=
:
,
又因为相似三角形的面积比等于相似比的平方,而△ABC的面积为
×2×1=1,
故△DEF和△GHI面积分别为0.5,5.故选B.

因为△DEF,△GHI和△ABC都相似,AB=
| 2 |
| 10 |
所以它们的相似比为DE:AB=1:
| 2 |
| 10 |
| 2 |
又因为相似三角形的面积比等于相似比的平方,而△ABC的面积为
| 1 |
| 2 |
故△DEF和△GHI面积分别为0.5,5.故选B.
点评:此题考查了相似三角形的性质:相似三角形的面积比等于相似比的平方.解此题还要注意格点三角形边长的求解方法:用勾股定理求解.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
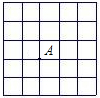 如图,小正方形的边长为1,若以A为顶点的等腰直角三角形的面积为
如图,小正方形的边长为1,若以A为顶点的等腰直角三角形的面积为| 5 |
| 2 |
| A、4个 | B、8个 |
| C、12个 | D、16个 |
 如图,小正方形的边长均为1,则下面图中的三角形(阴影部分)与△ABC相似的是( )
如图,小正方形的边长均为1,则下面图中的三角形(阴影部分)与△ABC相似的是( )
 (2012•北塘区二模)如图,小正方形的边长均为1,扇形OAB是某圆锥的侧面展开图,则这个圆锥的底面周长为( )
(2012•北塘区二模)如图,小正方形的边长均为1,扇形OAB是某圆锥的侧面展开图,则这个圆锥的底面周长为( ) 如图,小正方形的边长为1,试在图中作出2条长度不是有理数的线段和两条长度是有理数的线段.
如图,小正方形的边长为1,试在图中作出2条长度不是有理数的线段和两条长度是有理数的线段.