题目内容
【题目】(1)问题探究
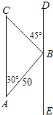
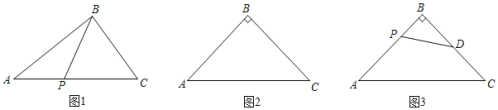
①如图1,在直角△ABC中,∠ABC=90°,AC=5,BC=3,P是AC边上一点,连接BP,则BP的最小值为 .
②如图2,在等腰直角△ABC中,∠ABC=90°,AC=a,求边AB的长度(用含a的代数式表示).
(2)问题解决
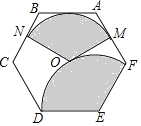
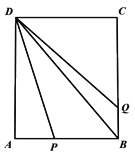
如图3,在等腰直角△ABC中,∠ABC=90°,AC=2![]() ,D是边BC的中点,若P是AB边上一点,试求:PD+
,D是边BC的中点,若P是AB边上一点,试求:PD+![]() AP的最小值.
AP的最小值.
【答案】(1)①![]() ;②
;②![]() ;(2)
;(2)![]() .
.
【解析】
(1)①作BE⊥AC于E,先利用勾股定理求出AB,再利用面积法求出BE,由此得到BP的最小值为BE的长;
②利用AC=a根据勾股定理即可求出AB的长度;
(2)作AH⊥AC,PE⊥AH于E,DF⊥AH于F交AB于T,利用等腰直角三角形的性质得到BT=BD=AT=1,DT=![]() ,再求出TF=
,再求出TF=![]() 得到DP+
得到DP+![]() PA=DP+PE,由此得到DP+PE最小值为DF的长,计算DF即可得到答案.
PA=DP+PE,由此得到DP+PE最小值为DF的长,计算DF即可得到答案.
(1)①如图1中,作BE⊥AC于E.
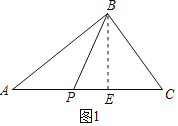
在Rt△ABC中,∵∠ABC=90°,AC=5,BC=3,
∴AB= ![]() ,
,
∵S△ABC=![]() ACBE=
ACBE=![]() ABBC,
ABBC,
∴BE=![]() ,
,
根据垂线段最短可知当BP与BE重合时,PB的值最小,最小值为![]() ,
,
故答案为![]() .
.
②如图2中,
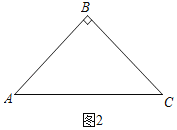
∵∠B=90°,AB=BC,
∴AB2+BC2=AC2,
∴AB2=![]() a2,
a2,
∴AB=![]() 或﹣
或﹣![]() (舍弃),
(舍弃),
∴AB=![]() ;
;
(2)如图3中,作AH⊥AC,PE⊥AH于span>E,DF⊥AH于F交AB于T.
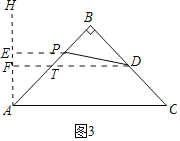
∵△ABC是等腰直角三角形,AC=2![]() ,
,
∴AB=BC=2,∠BAC=∠C=45°,
∵点D是BC的中点,
∴BD=CD=1,
∵DF⊥AH,AC⊥AH,
∴DF∥AC,
∴∠BTD=∠BAC=45°,∠BDT=∠C=45°,
∴∠BTD=∠BDT,
∴BT=BD=AT=1,DT=![]() ,
,
∵AH⊥AC,∠BAC=45°,
∴∠HAC=90°,∠HAT=45°,
∴AF=TF=![]() ,
,
∴PE=![]() PA,
PA,
∴DP+![]() PA=DP+PE,
PA=DP+PE,
根据垂线线段最短可知,当点E与F重合时,PD+![]() PA的值最小,最小值为DF的长=
PA的值最小,最小值为DF的长=![]() +
+![]() =
=![]() .
.