题目内容
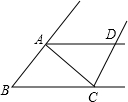
 如图,∠ABC=∠DCB=70°,∠ABD=40°,AB=DC,则∠BAC=
如图,∠ABC=∠DCB=70°,∠ABD=40°,AB=DC,则∠BAC=
- A.70°
- B.80°
- C.100°
- D.90°
B
分析:根据已知条件,可知四边形为等腰梯形,再根据其性质,可推出∠BAC=80°.
解答:因为梯形ABCD是等腰梯形,
则AC=BD,∠DBC=∠ACB=30°,
则∠BOC=120°
又因为∠BOC=∠BAC+∠ABD,
所以∠BAC=120°-40°=80°
故选B.
点评:此题主要考查学生对等腰梯形的性质的掌握情况.
分析:根据已知条件,可知四边形为等腰梯形,再根据其性质,可推出∠BAC=80°.
解答:因为梯形ABCD是等腰梯形,
则AC=BD,∠DBC=∠ACB=30°,
则∠BOC=120°
又因为∠BOC=∠BAC+∠ABD,
所以∠BAC=120°-40°=80°
故选B.
点评:此题主要考查学生对等腰梯形的性质的掌握情况.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
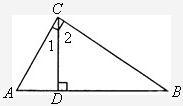
 如图,△ABC的两个外角的平分线相交于D,若∠B=50°,则∠ADC=( )
如图,△ABC的两个外角的平分线相交于D,若∠B=50°,则∠ADC=( )| A、60° | B、80° | C、65° | D、40° |
 ,且CB=CE.
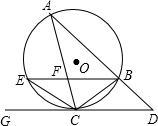
,且CB=CE. 5、已知:如图,△ABC内接于⊙O,AE切⊙O于点A,BD∥AE交AC的延长线于点D,求证:AB2=AC•AD.
5、已知:如图,△ABC内接于⊙O,AE切⊙O于点A,BD∥AE交AC的延长线于点D,求证:AB2=AC•AD.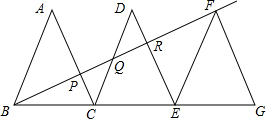 如图,△ABC、△DCE、△FEG是全等的三个等腰三角形,底边BC、CE、EG在同一直线上,且
如图,△ABC、△DCE、△FEG是全等的三个等腰三角形,底边BC、CE、EG在同一直线上,且