Question

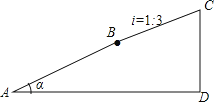
【题目】小林从点A出发，沿着坡角为α的斜坡向上走了650米到达点B，且sinα=．然后又沿着坡度i=1：3的斜坡向上走了500米达到点C．

（1）小明从A点到B点上升的高度是多少米？

（2）小明从A点到C点上升的高度CD是多少米？（结果保留根号）

Answer 1

【答案】（1）小明从A点到点B上升的高度是200米；（2）点C相对于起点A升高了（50+200）米．

【解析】

（1）根据题意画出图形，进而利用锐角三角函数关系求出BF；

（2）利用坡度的定义求得CE的长，即可得出点C相对于起点A升高的高度．

解：（1）如图所示：过点B作BF⊥AD于点F，BE⊥CD于点E，过点C作CD⊥AD于点D，

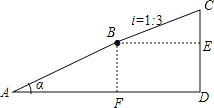
由题意得：AB=650米，BC=500米，

∴sinα===，

∴BF=650×=200米，

∴小明从A点到点B上升的高度是200米；

（2）∵斜坡BC的坡度为：1：3，

∴CE：BE=1：3，

设CE=x，则BE=3x，

由勾股定理得：x2+（3x）2=5002

解得：x=50，

∴CD=CE+DE=BF+CE=200+50，

答：点C相对于起点A升高了（50+200）米．

故答案为：（1）小明从A点到点B上升的高度是200米；（2）点C相对于起点A升高了（50+200）米．