题目内容
⊙O的直径为10 cm，弦AB的弦心距为3cm，则以弦AB为一边的⊙O内接矩形的周长为
- A.14cm
- B.28cm
- C.48cm
- D.20cm
B
分析：如图，根据垂径定理和勾股定理求AB、AC的长度，再求周长．
解答：
解：如图，
∵⊙O的直径为10 cm，弦AB的弦心距为3cm，
∴连接OA，OA=5cm，在Rt△AOG中，OA=5cm，OG=3cm，
故AG=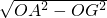
=
=4．根据垂径定理得，AB=2AG=2×4=8cm．
连接BC，则BC=10cm，在Rt△ABC中，BC=10cm，AB=8cm．
由勾股定理得AC=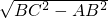
=
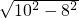=6．
故以弦AB为一边的⊙O内接矩形的周长为2AC+2AB=2×6+2×8=28cm．
故选B．
点评：本题属中等难度，涉及到垂径定理及勾股定理的运用．
分析：如图，根据垂径定理和勾股定理求AB、AC的长度，再求周长．
解答：
解：如图，∵⊙O的直径为10 cm，弦AB的弦心距为3cm，
∴连接OA，OA=5cm，在Rt△AOG中，OA=5cm，OG=3cm，
故AG=
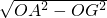==4．根据垂径定理得，AB=2AG=2×4=8cm．连接BC，则BC=10cm，在Rt△ABC中，BC=10cm，AB=8cm．
由勾股定理得AC=
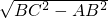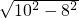==6．故以弦AB为一边的⊙O内接矩形的周长为2AC+2AB=2×6+2×8=28cm．
故选B．
点评：本题属中等难度，涉及到垂径定理及勾股定理的运用．
练习册系列答案
相关题目
如图，⊙O的直径为10，弦AB的长为6，M是弦AB上的一动点，则线段的OM的长的取值范围是（ ）| A、3≤OM≤5 | B、4≤OM≤5 | C、3＜OM＜5 | D、4＜OM＜5 |
如图，⊙O的直径为10，圆心O到弦AB的距离OM的长为3，则弦AB的长．