题目内容
在?ABCD中,AB=10,∠ABC=60°,以AB为直径作⊙O,边CD切⊙O于点E.(1)圆心O到CD的距离是______.
(2)求由弧AE、线段AD、DE所围成的阴影部分的面积.(结果保留π和根号)

【答案】分析:(1)连接OE,则OE的长就是所求的量;
(2)阴影部分的面积等于梯形OADE的面积与扇形OAE的面积的差.
解答:解:(1)连接OE.
∵边CD切⊙O于点E.
∴OE⊥CD
则OE就是圆心O到CD的距离,则圆心O到CD的距离是 ×AB=5.
×AB=5.
故答案是:5;
(2)∵四边形ABCD是平行四边形.
∴∠C=∠DAB=180°-∠ABC=120°,
∴∠BOE=360°-90°-60°-120°=90°,
∴∠AOE=90°,
作EF∥CB,∴∠OFE=∠ABC=60°,
在直角三角形OEF中,OE=5,
∴OF=OE•tan30°= .EC=BF=5-
.EC=BF=5- .
.
则DE=10-5+ =5+
=5+ ,
,
则直角梯形OADE的面积是: (OA+DE)×OE=
(OA+DE)×OE= (5+5+
(5+5+ )×5=25+
)×5=25+ .
.
扇形OAE的面积是: =
= .
.
则阴影部分的面积是:25+ -
- .
.
点评:本题主要考查了扇形的面积的计算,正确作出辅助线,把阴影部分的面积转化为梯形OADE的面积与扇形OAE的面积的差是解题的关键.
(2)阴影部分的面积等于梯形OADE的面积与扇形OAE的面积的差.
解答:解:(1)连接OE.
∵边CD切⊙O于点E.
∴OE⊥CD
则OE就是圆心O到CD的距离,则圆心O到CD的距离是
 ×AB=5.
×AB=5.故答案是:5;
(2)∵四边形ABCD是平行四边形.

∴∠C=∠DAB=180°-∠ABC=120°,
∴∠BOE=360°-90°-60°-120°=90°,
∴∠AOE=90°,
作EF∥CB,∴∠OFE=∠ABC=60°,
在直角三角形OEF中,OE=5,
∴OF=OE•tan30°=
 .EC=BF=5-
.EC=BF=5- .
.则DE=10-5+
 =5+
=5+ ,
,则直角梯形OADE的面积是:
 (OA+DE)×OE=
(OA+DE)×OE= (5+5+
(5+5+ )×5=25+
)×5=25+ .
.扇形OAE的面积是:
 =
= .
.则阴影部分的面积是:25+
 -
- .
.点评:本题主要考查了扇形的面积的计算,正确作出辅助线,把阴影部分的面积转化为梯形OADE的面积与扇形OAE的面积的差是解题的关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
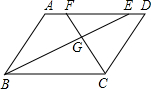 如图,在?ABCD中,AB=5,BC=8,∠ABC,∠BCD的角平分线分别交AD于E和F,BE与CF交于点G,则△EFG与△BCG面积之比是( )
如图,在?ABCD中,AB=5,BC=8,∠ABC,∠BCD的角平分线分别交AD于E和F,BE与CF交于点G,则△EFG与△BCG面积之比是( )| A、5:8 | B、25:64 | C、1:4 | D、1:16 |
 如图所示,在?ABCD中,AB=2AD,∠A=60°,E,F分别为AB,CD的中点,EF=1cm,那么对角线BD的长度为
如图所示,在?ABCD中,AB=2AD,∠A=60°,E,F分别为AB,CD的中点,EF=1cm,那么对角线BD的长度为 s的速度沿AB向终点B运动,当它们有一个到达终点时,另一个也随之停止运动,设运动时间为ts.
s的速度沿AB向终点B运动,当它们有一个到达终点时,另一个也随之停止运动,设运动时间为ts.