题目内容
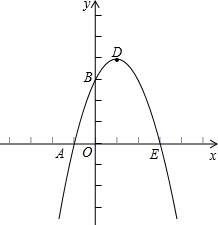 如图,已知抛物线与x交于A(-1,0)、E(3,0)两点,与y轴交于点B(0,3).
如图,已知抛物线与x交于A(-1,0)、E(3,0)两点,与y轴交于点B(0,3).(1)求抛物线的解析式;
(2)设抛物线顶点为D,△AOB与△DBE是否相似?如果相似,请给以证明;如果不相似,请说明理由.
(3)若点P为第一象限抛物线上一动点,连接BP、PE,求四边形ABPE面积的最大值,并求此时P点的坐标.
分析:(1)根据B的坐标求出c,设抛物线解析式为y=ax2+bx+3,把A、E的坐标代入得出方程组,求出方程组的解即可;
(2)根据点的坐标和勾股定理求出BD、DB、DE的长,根据勾股定理的逆定理求出∠DBE=90°,求出
=
,根据相似三角形的判定求出即可;
(3)四边形ABPE的面积等于△AOB的面积加上四边形BOQP的面积加上△PQE的面积,根据面积公式代入求出,化成二次函数的顶点式,即可求出答案.
(2)根据点的坐标和勾股定理求出BD、DB、DE的长,根据勾股定理的逆定理求出∠DBE=90°,求出
| AO |
| BD |
| BO |
| BE |
(3)四边形ABPE的面积等于△AOB的面积加上四边形BOQP的面积加上△PQE的面积,根据面积公式代入求出,化成二次函数的顶点式,即可求出答案.
解答:解:(1)∵抛物线与y轴交于点(0,3),
∴设抛物线解析式为y=ax2+bx+3,
根据题意得:
,
解得:
,
∴抛物线的解析式是y=-x2+2x+3.
解法二、∵设解析式是y=a(x-3)(x+1),
把B(0,3)代入得:3=a(0-3)(0+1),
a=-1,
即y=-1(x-3)(x+1)=-x2+2x+3,
∴抛物线的解析式是y=-x2+2x+3.
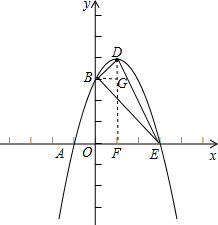
(2)相似,
证明:过D作DF⊥x轴于F,过B作BG⊥DF于G,
如图,BD=
=
=
,BE=
=
=3
,
DE=
=
=2
,
∴BD2+BE2=20,DE2=20,
∴DB2+BE2=DE2,
∴△BDE是直角三角形,
∴∠AOB=∠DBE=90°,且
=
=
,
∴△AOB∽△DBE.
(3)解:设点P的坐标为(x,y),过P作PQ⊥X轴于Q,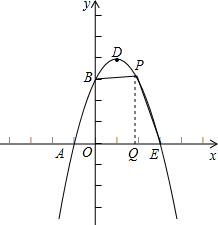
则SABPE=S△ABO+SBOQP+S△PQE=
×1×3+
×(3+y)×x+
×y×(3-x)=-
x2+
x+6=-
(x-
)2+9
,
当x=
时,四边形ABPE面积最大,
此时,点P的坐标为(
,
).
∴设抛物线解析式为y=ax2+bx+3,
根据题意得:
|
解得:
|
∴抛物线的解析式是y=-x2+2x+3.
解法二、∵设解析式是y=a(x-3)(x+1),
把B(0,3)代入得:3=a(0-3)(0+1),
a=-1,
即y=-1(x-3)(x+1)=-x2+2x+3,
∴抛物线的解析式是y=-x2+2x+3.

(2)相似,
证明:过D作DF⊥x轴于F,过B作BG⊥DF于G,
如图,BD=
| BG2+DG2 |
| 12+12 |
| 2 |
| BO2+OE2 |
| 32+32 |
| 2 |
DE=
| DF2+EF2 |
| 22+42 |
| 5 |
∴BD2+BE2=20,DE2=20,
∴DB2+BE2=DE2,
∴△BDE是直角三角形,
∴∠AOB=∠DBE=90°,且
| AO |
| BD |
| BO |
| BE |
| ||
| 2 |
∴△AOB∽△DBE.
(3)解:设点P的坐标为(x,y),过P作PQ⊥X轴于Q,

则SABPE=S△ABO+SBOQP+S△PQE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 9 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 8 |
当x=
| 3 |
| 2 |
此时,点P的坐标为(
| 3 |
| 2 |
| 15 |
| 4 |
点评:本题考查了勾股定理及逆定理,二次函数的最值,用待定系数法求二次函数的解析式,三角形的面积,相似三角形的判定等知识点的运用,解此题的关键是综合运用性质进行推理和计算,题型较好,通过做此题培养了学生的计算能力和观察图形的能力.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
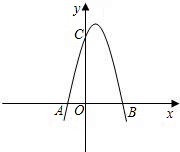 如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).
如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).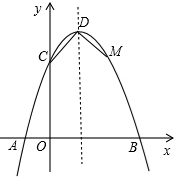 如图,已知抛物线与x轴交于点A(-1,0),与y轴交于点C(0,3),且对称轴方程为x=1
如图,已知抛物线与x轴交于点A(-1,0),与y轴交于点C(0,3),且对称轴方程为x=1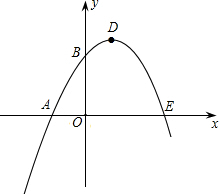 函数的最大值是4.
函数的最大值是4. (2012•株洲)如图,已知抛物线与x轴的一个交点A(1,0),对称轴是x=-1,则该抛物线与x轴的另一交点坐标是( )
(2012•株洲)如图,已知抛物线与x轴的一个交点A(1,0),对称轴是x=-1,则该抛物线与x轴的另一交点坐标是( )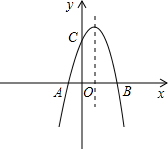 如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).
如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).