题目内容
已知一靶中心50环的半径r=10cm,30环的半径R1=20cm,10环的半径R2=40cm,如果每弹都打在靶上并取得环数,求:(1)击中靶上50环的可能性;(2)击中30环或50环的可能性;(3)击中10环的可能性.
解:整个圆环的面积为π×402=1600π.
(1)中心50环的面积为π×102=100π,
故击中中心50环的概率为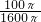 =
= ;
;
(2)中心30环的面积为π×202=400π,
击中靶上30环或50环的可能性为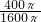 =
= ;
;
(3)击中10环的可能性为1- =
= .
.
分析:要求可能性的大小,只需求出各自所占的比例大小即可.求比例时,应注意记清各自的数目.
点评:用到的知识点为:可能性等于所求情况数与总情况数之比.
(1)中心50环的面积为π×102=100π,
故击中中心50环的概率为
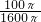 =
= ;
;(2)中心30环的面积为π×202=400π,
击中靶上30环或50环的可能性为
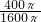 =
= ;
;(3)击中10环的可能性为1-
 =
= .
.分析:要求可能性的大小,只需求出各自所占的比例大小即可.求比例时,应注意记清各自的数目.
点评:用到的知识点为:可能性等于所求情况数与总情况数之比.

练习册系列答案
相关题目

